2.7.8 Methods of magnet probe parameters estimation
+1-480-493-0093

2.7.8 Methods of magnet probe parameters estimation

At the present time there are a lot of MFM probes of various types [1]. The proper choice of a probe for studying a specific microstructure is sometimes an independent and complicated problem and is determined by a researcher experience. To simplify the problem, one needs to have techniques that allow to quantify magnetic characteristics of probes, the major of which are the magnetic moment per unit volume of a film (magnetization) and magnetic coating coercivity.

To characterize probes, many methods were proposed from analysis of their interaction with a hard disk or magnetic tape surface [2], including measurements of magnetic heads field [3] to even exotic technique connected with studying the magnetotactical bacteria [4]. However, the simplest from the standpoint of interpretation is the technique of the interaction detection between the tip and the magnetic field of a current-carrying microconductor. The magnetic field of such systems can be calculated with a high accuracy using methods of conventional magnetostatics even in an analytic form in most cases.

In [5] it was proposed to use a straight current carrying strip line for this purpose. The scanning was performed across the strip in the presence of external magnetic field. Determined was the coercitive field (along and across the tip) for the following coatings 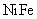, 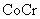(150A, 400A), 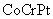, 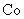. Also, the authors of [5] succeeded in estimating an effective magnetic moment. However, in [6] the role of the electrostatic interaction with a conductor was revealed and a method of electrostatic and magnetic interaction separation was proposed. Though in [5] the electrostatic interaction was not taken into account, the sample was prepared very thoroughly. In particular, a thin layer of gold several tens of angstrom thick was deposited over a dielectric layer. The golden coating was connected to the ground potential that apparently minimized the electrostatic interaction of a probe with a current-carrying conductor.

Further development of magnetic probe calibration techniques led to the use of a current 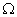-ring magnetic field. In [7] the rings of diameter 1-5 micron and strip width of 200 nm manufactured by submicron lithography were first used for the magnetic tip calibration. However, the qualitative analysis of the experiment was not quite correct, in particular because the authors used the model of a point dipole assuming that it was situated precisely at the tip end. As is shown in [8], such assumption results, after accurate data processing, in unreasonable magnitudes of effective monopole and dipole. A more accurate experiment [8] permitted to determine the magnitude of magnetic dipole and its location inside the sample. It was shown experimentally that the effective dipole should be located approximately in the center of an area whose vertical dimension depends on characteristic attenuation length of magnetic field. This length is proportional to the ring radius. In this case, the cantilever magnetic moment becomes dependent on the radius of the ring used in experiment. A theoretical calculation by integration over the interaction region under the assumption that the magnetic moment of the film unit volume is equal to macroscopic saturation magnetization of the coating material, gives a reasonable agreement with measurement results.

Thus, the effective moment of the tip with magnetic coating depends on what kind of magnetic structure is studied. Therefore, for such tips it is reasonable to measure and tabulate not the magnetic moment of the tip but the magnetic moment per unit area of a coating film. On the other hand, determination of the total magnetic moment for tips with localized magnetic moment [9-12] is quite reasonable and in this case its location is determined unambiguously.

To measure the hysteresis loop of tips magnetic coatings, in [13] it is proposed to place the whole cantilever in a magnetic field with changing gradient (external coil produces field of 0.2 Oe) and frequency close to the cantilever resonant frequency. Measuring the amplitude of oscillations, the force magnitude was estimated and the magnetic moment was determined in relative units. Varying the external field by permanent magnet (up to 280 Oe), the authors measured the hysteresis loop for such coatings as , , .

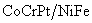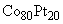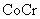In chapter 2.7.4 and 2.7.5 the technique of determination of point dipole and monopole effective value is described in detail. However, as it is pointed out before, the quantitative characteristic of point dipole (monopole) and its location in a probe depend much on the attenuation length of a studied sample magnetic field. Therefore, in order to unambiguously calibrate the magnetic probe it is necessary to measure the magnetization of the probe ferromagnetic hard magnetic material.

For this purpose, a special Flash model was developed which calculates theoretically the change in amplitude, phase and frequency of a probe oscillation or the static deflection of a probe during the second pass across a sample surface in the standard AC MFM mode. In this model the current-carrying rectangular conductor acts as the sample for study. The spatial distribution of magnetic field produced by the current in a rectangular strip is obtained in chapter 2.7.9.

Utilizing a general case of the model of a hard magnetic probe interaction with a sample magnetic field (see chapter 2.7.3), a theoretical analysis of the current-carrying strip magnetic field interaction with probes of various types: cylindrical, spherical, conical, and diamagnetic conical with ferromagnetic coating is performed (see chapter 2.7.9 and Appendices for it). The models allow to study the effect of variation of sample geometry, probe parameters (dimensions, magnetization, stiffness, resonant frequency, quality factor), measurement mode parameters within permissible limits. The calculation of the amplitude, phase and frequency change is performed in accordance with formulas (18), (16), (11) of chapter 2.3.4.

Thus, substituting the experimental data of the strip line magnetic field MFM measurements in AC mode into this Flash model, it is possible to compare them with theoretical ones at various probe and sample parameters. Hence, using this model, one can determine unknown parameters of the probe (magnetization, in particular) by varying model parameters until experimental and theoretical data fit well. Moreover, a set of optimal parameters can be selected that provides the maximum change of detected signals from given samples.

 

Summary.

  • A review of magnetic probes calibration methods and accompanying problems is presented.
  • The most widespread and simple enough technique of a probe magnetic characteristics determination is its calibration in the magnetic field of a current-carrying microconductor.
  • Presented are the theoretical aspects of a Flash model which allow to calculate the measured in a standard AC MFM mode parameters depending on the sample parameters (strip line/-ring).
  • By means of the developed Flash model one can determine unknown probe parameters appearing in an experiment and choose an optimal set of a system theoretical parameters that provides the maximum change in detected signals.

References.

  1. P. Grutter, H.J. Mamin, D. Rugar, in Scanning Tunneling Microscopy II, edited by R. Wiesendanger and H.-J. Guntherodt (Springer, Berlin, 1992) pp. 151-207.
  2. D. Rugar, H.J. Mamin, P. Guethner et al, J. Appl. Phys. 68, 1169 (1990).
  3. S. Khizroev, W. Jayasekara, J. Bain et al, IEEE Trans. Magn. 34, 2030 (1998).
  4. R.B. Proksch, T.E. Shaffer, B.M. Moskowitz, Appl. Phys. Lett. 66, 2582 (1995).
  5. K.L. Babcock, V.B. Elings, J. Shi et al, Appl. Phys. Lett. 69, 705 (1996).
  6. T. Alvarez, S.V. Kalinin, D.A. Bonnell, Appl. Phys. Lett. 78, 1005 (2001).
  7. L. Kong, S.Y. Chou, Appl. Phys. Lett. 70, 2043 (1997).
  8. J. Lohau, S. Kirsch, A. Carl et al, J. Appl. Phys. 86, 3410 (1999).
  9. M.R. Koblischka, U. Hartmann, T. Sulzbach, Thin Solid Films 428, 93 (2003).
  10. T. Arie, H. Nishijima, S, Akita et al, J. Vac. Sci. Technol. B 18, 104 (2000).
  11. T. Arie, N. Yoshida, S. Akita et al, J. Phys. D 34, L34 (2001).
  12. N. Yoshida, T. Arie, S. Akita, Y. Nakayama, Physica B: Cond. Matt. 323, 149 (2002).
  13. J. Lohau, S. Kirsch, A. Carl et al, J. Appl. Phys. 86, 3410 (1999).