2.7.3 Interaction of the hard magnetic cantilever with the magnetic field of the studied sample (general case)
If we know the magnetic field
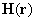 from the sample, then force
from the sample, then force
 acting on magnetic cantilever and its derivative
acting on magnetic cantilever and its derivative
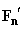 in
in
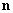 direction can be calculated by integrating the force acting on unit volume
direction can be calculated by integrating the force acting on unit volume
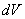 over the ferromagnetic film volume
over the ferromagnetic film volume
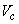 [1]:
[1]:
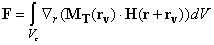
(1)
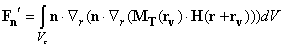
(2)
where
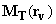 – magnetic moment per cantilever magnetic layer unit volume,
– magnetic moment per cantilever magnetic layer unit volume,
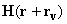 – magnetic field from the sample,
– magnetic field from the sample,
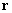 – vector corresponding to the tip position,
– vector corresponding to the tip position,
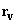 – vector corresponding to the elementary magnetic moment position relative to
– vector corresponding to the elementary magnetic moment position relative to
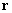 ,
,
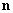 – normal vector to the probe surface collinear with its principal axis of symmetry (Fig. 1).
– normal vector to the probe surface collinear with its principal axis of symmetry (Fig. 1).
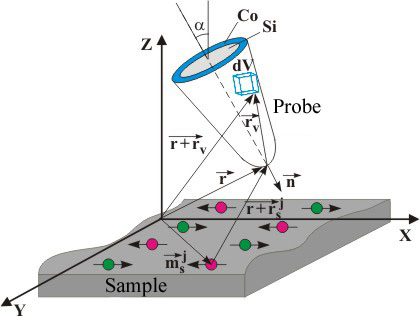
Fig. 1. Model geometry used to calculate force and its derivative acting on tip.
If vector
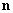 is directed along Z axis, then force (1) and its Z-derivative (2) are:
is directed along Z axis, then force (1) and its Z-derivative (2) are:
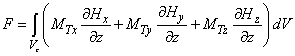
(3)
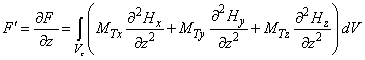
(4)
Magnetic field
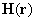 from the magnetic sample can be calculated in two ways. The sample is divided into elementary magnetic domains
from the magnetic sample can be calculated in two ways. The sample is divided into elementary magnetic domains
 and at any space point
and at any space point
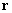 the magnetic field from every domain
the magnetic field from every domain
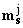 , which is determined by well known formula [2], is summed:
, which is determined by well known formula [2], is summed:
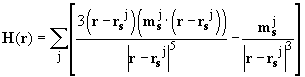
(5)
where
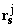 – distance from the point of origin to the sample magnetic domain
– distance from the point of origin to the sample magnetic domain
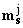 .
.
According to [3], magnetic field
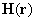 can be calculated from the following equation
can be calculated from the following equation
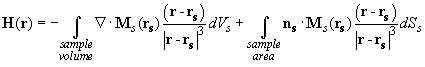
(6)
where
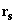 – distance from the point of origin to the sample magnetic domain
– distance from the point of origin to the sample magnetic domain
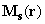 and
and
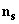 – normal vector to the sample surface. Substituting into equations (1), (2) instead of
– normal vector to the sample surface. Substituting into equations (1), (2) instead of
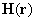 expressions (5) and (6), we can find
expressions (5) and (6), we can find
 and
and
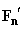 .
.
Summary.
- Described is a model that in a general case allows to calculate the force acting on the probe with known magnetic characteristics at a given point in space over the sample having arbitrary distribution of the magnetization vector and its derivative.
- This model is valid only for hard magnetic cantilevers and samples when mutual interference of sample
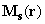 and probe
and probe
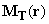 magnetization is not taken into consideration.
magnetization is not taken into consideration.
References.
- P. Grutter, H.J. Mamin, D. Rugar, in Scanning Tunneling Microscopy II, edited by R. Wiesendanger and H.-J. Guntherodt (Springer, Berlin, 1992) pp. 151-207.
- L.D. Landau, E.M. Lifshitz. Theoretical Physics, vol. 2, Field Theory, Nauka, 1973, 504 p. (in Russian).
- W.F. Brown. Magnetostatic Principles in Ferromagnetism (Amsterdam 1962).
- U. Hartmann. J. Appl. Phys. 64, 1561 (1988).






