2.7.5 Effective monopole magnetic charge approximation
Along with the model of point dipole (see chapter 2.7.4), an alternative model of point monopole charge exists which allows to describe in some cases the cantilever interaction with the magnetic field.
Consider the cylinder of length L and radius R uniformly magnetized along lateral surface in the z-axis direction as a magnetic probe (Fig. 1). Magnetic material in Fig.1 is cobalt.
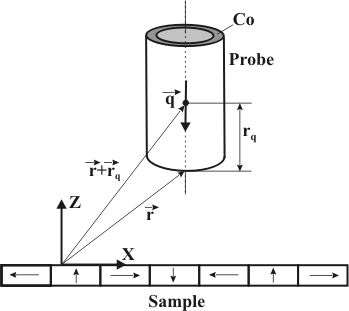
Fig. 1. On the monopole approximation.
Let the bottom end of the probe be at the point with radius-vector
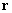. Denote
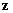as the unit vector along the z-axis. Suppose that the attenuation length of magnetic field
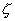is much less than L, then the magnetic field at the probe top end
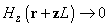. Moreover, let magnetic field vector
be almost independent on x and y at least within the distance of probe radius R. Then the force acting on the probe along z-axis in accordance with chapter 2.7.3 is given by:
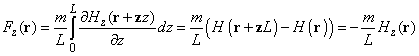
(1)
where m – total magnetic moment of the cylinder. If the probe is of finite length, i.e. condition
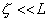is not met properly or probe section is not constant, the calculation and measurement agree well in case the point monopole is supposed to be placed some distance
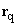from the probe end.
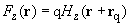
(2)
where
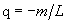– magnetic moment per cylinder unit length which is called the monopole charge.
In the point monopole model it is considered that the probe magnetic properties are completely defined by its effective magnetic monopole charge
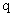and by position
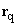of this resultant monopole inside the probe (Fig. 1). In this case, the force acting on the probe in the z-axis direction is proportional to the magnetic field magnitude and is given by (2) while its derivative is
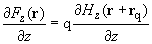
(3)
As can be seen from (2), the effective force just reflects the magnetic force distribution and force directional derivative – the field derivative correspondingly.
In practice, this model is used by analogy with the dipole model described in chapter 2.7.4. Using calibrating samples with known magnetic field distribution,
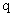and
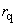parameters are varied to obtain the best agreement between theory and experiment. This model works well at large distances from the sample surface when the field changes slowly. However, like in case of dipole approximation, magnitudes of
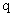and
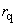must be different for samples with the field attenuation length different from that of the calibrating sample.
Summary.
- In the model of effective monopole magnetic charge it is considered that the probe magnetic properties are completely defined by its effective magnetic monopole charge
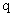and by position
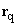of this resultant monopole inside the probe.
- It is difficult to quantify MFM data in the framework of this model because parameters of effective magnetic monopole are themselves dependent on the studied sample's magnetic characteristics.
- It is difficult to quantify MFM data in the framework of this model because parameters of effective magnetic monopole are themselves dependent on the studied sample's magnetic characteristics.
References.
- U. Hartmann, J. Physcs Letters A. 137, 475 (1989).
- J. Lohau, S. Kirsch, A. Carl et al, J. Appl. Phys. 86, 3410 (1999).
- P. Grutter, H.J. Mamin, D. Rugar, in Scanning Tunneling Microscopy II, edited by R. Wiesendanger and H.-J. Guntherodt (Springer, Berlin, 1992) pp. 151-207.