2.7.4 Dipole effective magnetic moment approximation
Within the framework of the point dipole model the probe magnetic properties are considered to be entirely defined by its dipole effective magnetic moment
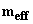 as well as by position
as well as by position
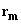 of this resultant moment inside the cantilever (Fig. 1).
of this resultant moment inside the cantilever (Fig. 1).
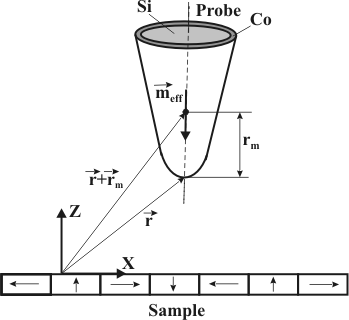
Fig. 1. Dipole model of point interaction between probe and magnetic field.
If the probe tip is perpendicular to the sample surface (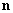 and Z are collinear, see Fig. 1), then expressions (3), (4) of chapter 2.7.3 in the point dipole approximation can be rewritten as:
and Z are collinear, see Fig. 1), then expressions (3), (4) of chapter 2.7.3 in the point dipole approximation can be rewritten as:
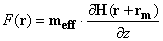
(1)
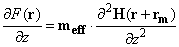
(2)
that is both
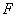 and
and
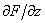 depend on the field magnitude only at conditional point
depend on the field magnitude only at conditional point
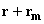 where dipole is placed.
where dipole is placed.
To determine field magnitudes that make point dipole model applicable, one should compare equations (1) of this section and (3) of chapter 2.7.3 written for the same field. Applicability criteria to within second derivatives is given by (simplified formula from [1]):
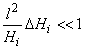
(3)
where
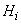 – field components (
– field components (
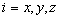 ), D – Laplacian, l – characteristic tip size (linear dimension of tip area interacting with magnetic field). This expression can be simplified as
), D – Laplacian, l – characteristic tip size (linear dimension of tip area interacting with magnetic field). This expression can be simplified as
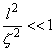
(4)
where
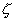 – characteristic scale of field variation, i.e. the distance at which the field changes are of its own order.
– characteristic scale of field variation, i.e. the distance at which the field changes are of its own order.
Model parameters
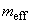 and
and
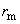 are determined experimentally for every cantilever. A calibration is performed in the known magnetic field. For this purpose, microscopic loops with flowing current and calculated magnetic field distribution [2] can be used. They are fabricated photolithographically on the sample surface. The force derivative
are determined experimentally for every cantilever. A calibration is performed in the known magnetic field. For this purpose, microscopic loops with flowing current and calculated magnetic field distribution [2] can be used. They are fabricated photolithographically on the sample surface. The force derivative
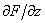 is measured at different heights above the sample surface. Then parameters
is measured at different heights above the sample surface. Then parameters
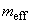 and
and
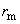 are varied to get the best agreement between measured
are varied to get the best agreement between measured
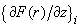 and calculated
and calculated
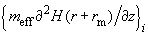 values.
values.
Despite the simplicity of this method of the cantilever calibration and further interpretation of MFM results, this model is applicable only to some cantilever types and magnetic samples. It was shown, that for samples with sufficiently different attenuation length of magnetic field but having the same field magnitude as that of the calibrating sample, values of
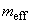 and
and
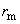 must be quite different. In [2] the dependence of
must be quite different. In [2] the dependence of
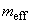 and
and
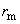 on attenuation length was studied using the calibrating W-shaped metallic loops at constant cantilever oscillation parameters. It is well known that the magnetic field on the axis of the ring with flowing direct current is inversely proportional to the ring radius and attenuation length is about the radius R. Table 1 presents dependences of
on attenuation length was studied using the calibrating W-shaped metallic loops at constant cantilever oscillation parameters. It is well known that the magnetic field on the axis of the ring with flowing direct current is inversely proportional to the ring radius and attenuation length is about the radius R. Table 1 presents dependences of
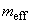 and
and
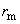 on radius of studied rings [2].
on radius of studied rings [2].
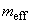 , A2 , A2 |
R, m | 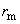 , m , m |
l, m |
| 6,009·10–15 | 6,030·10–7 | 5,2·10–7 | 9,285·10–7 |
| 4,744·10–14 | 1,419·10–6 | 1,31·10–6 | 2,564·10–6 |
| 2,042·10–13 | 2,369·10–6 | 2,86·10–6 | 5,292·10–6 |
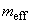 ,
,
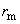 and l at various R
and l at various R
In table 1 parameter l stands for the tip length counted off from its end and contributing to the interaction with the magnetic field. In [2] it is determined as follows. First, the tip magnetization is measured using superconducting quantum magnetometer and magnetic moment per tip coating unit volume is calculated. Then, considering the tip as a regular quadrangular pyramid, integration is performed to determine the sum magnetic moment. The region of integration l is varied to fit the experimental value of
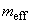 . From table 1 it follows that l is a linear function of the ring radius R and hence is proportional to attenuation length
. From table 1 it follows that l is a linear function of the ring radius R and hence is proportional to attenuation length
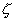 .
.
In that way, since effective magnetic dipole depends on sample magnetic characteristics, it is problematic to quantify MFM data for classical silicon tips with magnetic coating. Nevertheless, this model is useful for qualitative interpretation of measurement results or for quantifying data obtained with tips made of magnetic nanoparticles.
Summary.
- In the dipole effective magnetic moment model it is considered that tip magnetic properties are entirely defined by its effective magnetic dipole moment
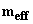 and position
and position
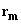 of this resultant moment inside the cantilever.
of this resultant moment inside the cantilever. - This model is applicable for qualitative analysis of MFM data in case of meeting the conditions (3), (4).
- Quantitative analysis of MFM results is difficult because parameters of effective magnetic dipole themselves are dependent on the studied sample magnetic characteristics.
References.
- U. Hartmann, J. Physcs Letters A. 137, 475 (1989).
- J. Lohau, S. Kirsch, A. Carl et al, J. Appl. Phys. 86, 3410 (1999).
- P. Grutter, H.J. Mamin, D. Rugar, in Scanning Tunneling Microscopy II, edited by R. Wiesendanger and H.-J. Guntherodt (Springer, Berlin, 1992) pp. 151-207.






