Appendices
Appendix 1. Calculation of the force and force gradient on a cylindrical
ferromagnetic probe in the magnetic field of a ring with current.
Let us determine the force and derivative of the force acting on cylindrical ferromagnetic tip of radius
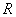 , length
, length
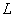 and magnetization
and magnetization
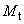 placed in a magnetic field of a current-carrying conductor. Let magnetization vector
placed in a magnetic field of a current-carrying conductor. Let magnetization vector
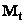 be directed throughout the tip volume on the angle
be directed throughout the tip volume on the angle
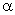 to the cylinder base normal (Fig. 1).
to the cylinder base normal (Fig. 1).
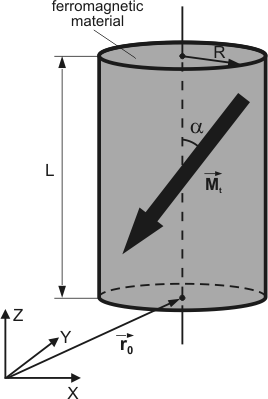
Fig. 1. Schematic representation of a cylindrical probe.
Vector
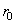 has coordinates
has coordinates
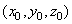 .
.
As shown in chapter 2.7.3, force
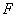 acting on magnetic cantilever and its derivative
acting on magnetic cantilever and its derivative
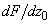 can be calculated integrating the force acting on the elementary volume over all the ferromagnetic material. It shall be convenient to perform the integration of an arbitrary function
can be calculated integrating the force acting on the elementary volume over all the ferromagnetic material. It shall be convenient to perform the integration of an arbitrary function
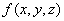 over the cylinder volume in cylindrical coordinates
over the cylinder volume in cylindrical coordinates
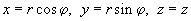 which gives
which gives
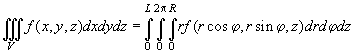
(1)
Thus, changing variables
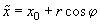 ,
,
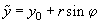 ,
,
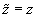 we find that the force and its Z-derivative in accordance with formulas (1, 2) in chapter 2.7.3 and (1) are determined through function
we find that the force and its Z-derivative in accordance with formulas (1, 2) in chapter 2.7.3 and (1) are determined through function
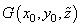 as follows
as follows
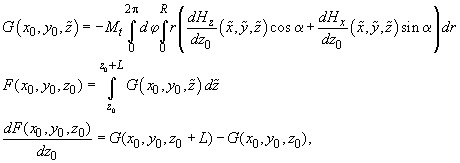
(2)
where derivatives of magnetic field
 in analytic form are given by formulas (6,7) in chapter 2.7.10.
in analytic form are given by formulas (6,7) in chapter 2.7.10.
Appendix 2. Calculation of the force and force gradient on a spherical
ferromagnetic tip in the magnetic field of a ring with current.
Let us determine the force and derivative of the force acting on spherical ferromagnetic tip of radius
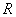 and magnetization
and magnetization
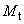 placed in a magnetic field of a current ring. Let the magnetization vector
placed in a magnetic field of a current ring. Let the magnetization vector
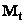 be directed on the angle
be directed on the angle
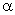 to the Z-axis (Fig. 2).
to the Z-axis (Fig. 2).
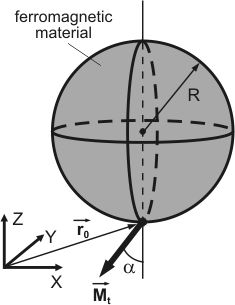
Fig. 2. Schematic representation of a spherical probe.
Vector
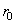 has coordinates
has coordinates
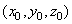 .
.
As shown in chapter 2.7.3, force
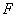 acting on magnetic cantilever and its derivative
acting on magnetic cantilever and its derivative
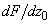 can be calculated integrating the force acting on the elementary volume over all the ferromagnetic material. It shall be convenient to perform the integration of an arbitrary function
can be calculated integrating the force acting on the elementary volume over all the ferromagnetic material. It shall be convenient to perform the integration of an arbitrary function
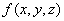 over the sphere volume in spherical coordinates
over the sphere volume in spherical coordinates
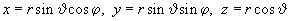 which gives
which gives
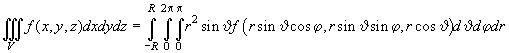
(3)
Thus, changing variables
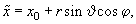 ,
,
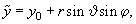 ,
,
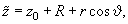 we find that the force and its Z-derivative in accordance with formulas (1, 2) in chapter 2.7.3 and (3) are determined as follows
we find that the force and its Z-derivative in accordance with formulas (1, 2) in chapter 2.7.3 and (3) are determined as follows
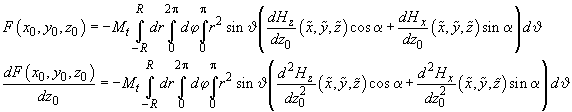
(4)
where derivatives of magnetic field  in analytic form are given by formulas (6,7) in chapter 2.7.10.
in analytic form are given by formulas (6,7) in chapter 2.7.10.
Appendix 3. Calculation of the force and force gradient on a conical tip covered
with a ferromagnetic film in the magnetic field of a current ring.
Let us determine the force and derivative of the force acting on a conical tip covered with a ferromagnetic film placed in a magnetic field of a current-carrying ring. The tip has radius
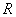 , length
, length
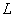 and cone angle
and cone angle
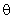 ; the ferromagnetic film has thickness
; the ferromagnetic film has thickness
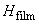 and magnetization
and magnetization
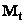 directed along the Z-axis (Fig. 3).
directed along the Z-axis (Fig. 3).
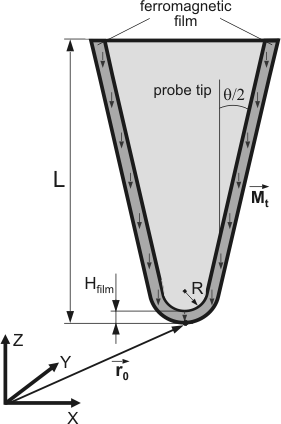
Fig. 3. Section of a conical probe covered with a ferromagnetic film.
Vector
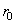 has coordinates
has coordinates
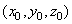 .
.
As shown in chapter 2.7.3, force
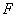 acting on magnetic cantilever and its derivative
acting on magnetic cantilever and its derivative
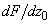 can be calculated integrating the force acting on the elementary volume over all the ferromagnetic material. It shall be convenient to perform the volume integration in two steps.
can be calculated integrating the force acting on the elementary volume over all the ferromagnetic material. It shall be convenient to perform the volume integration in two steps.
The first step is the determination of the force and its derivative acting on the spherical part of the tip. For the sake of mathematical convenience we will perform the integration over the sphere volume in spherical coordinates (see Appendix 2). Thus, changing variables
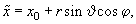
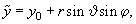
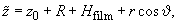 we find that the force and its Z-derivative on the spherical part of the tip in accordance with formulas (1, 2) in chapter 2.7.3 are determined as follows
we find that the force and its Z-derivative on the spherical part of the tip in accordance with formulas (1, 2) in chapter 2.7.3 are determined as follows
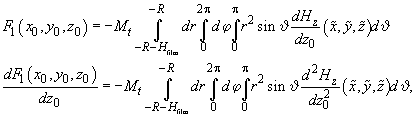
(5)
where derivatives of magnetic field  in analytic form are given by formulas (6,7) in chapter 2.7.10.
in analytic form are given by formulas (6,7) in chapter 2.7.10.
The second step is the determination of the force and its derivative acting on the remaining part of ferromagnetic film between two cones. In this case, it is convenient to perform the integration in cylindrical coordinates (see Appendix 1) with a changing radius of integration that depends on the Z-coordinate. Thus, changing variables
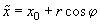 ,
,
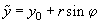 ,
,
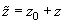 we find that the force and its Z-derivative acting on the nonspherical part of the tip in accordance with formulas (1, 2) in chapter 2.7.3 are determined as follows
we find that the force and its Z-derivative acting on the nonspherical part of the tip in accordance with formulas (1, 2) in chapter 2.7.3 are determined as follows
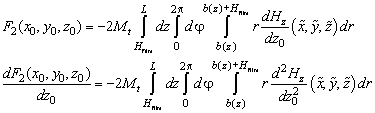
(6)
where
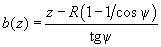 и
и
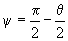 .
.
The total force and its derivative on this tip are then given by:
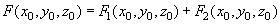
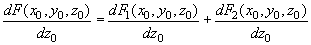
(7)
Appendix 4. Calculation of the force and force gradient on a conical
ferromagnetic probe in the magnetic field of a ring with current.
Let us determine the force and derivative of the force acting on a conical ferromagnetic tip placed in the magnetic field of a current carrying ring. The tip has radius
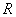 , length
, length
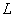 and cone angle
and cone angle
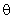 ; its magnetization
; its magnetization
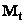 is directed at angle of
is directed at angle of
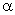 to the Z-axis (Fig. 4).
to the Z-axis (Fig. 4).
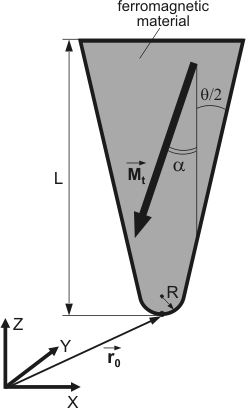
Fig. 4. Section of a conical ferromagnetic probe.
Vector
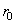 has coordinates
has coordinates
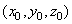 .
.
As shown in chapter 2.7.3, force
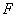 acting on magnetic cantilever and its derivative
acting on magnetic cantilever and its derivative
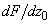 can be calculated integrating the force acting on the elementary volume over all the ferromagnetic material. It shall be convenient to perform the volume integration in two steps.
can be calculated integrating the force acting on the elementary volume over all the ferromagnetic material. It shall be convenient to perform the volume integration in two steps.
The first step is the determination of the force and its derivative acting on the spherical part of the tip. It is convenient to perform the integration over the sphere volume in spherical coordinates (see Appendix 2). Thus, changing variables
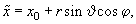
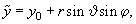
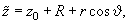 we find that the force and its Z-derivative acting on the spherical part of the tip in accordance with formulas (1, 2) in chapter 2.7.3 are determined as follows
we find that the force and its Z-derivative acting on the spherical part of the tip in accordance with formulas (1, 2) in chapter 2.7.3 are determined as follows
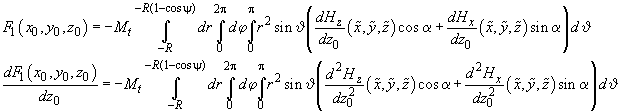
(8)
where
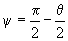 and derivatives of magnetic field
and derivatives of magnetic field
 in analytic form are given by formulas (6,7) in chapter 2.7.10.
in analytic form are given by formulas (6,7) in chapter 2.7.10.
The second step is the determination of the force and its derivative acting on the cone excluding its spherical part. In this case, it is convenient to perform the integration in cylindrical coordinates (see Appendix 1) with a changing radius of integration that depends on the Z-coordinate. Thus, changing variables
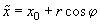 ,
,
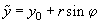 ,
,
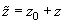 we find that the force and its Z-derivative acting on the conical part of the tip in accordance with formulas (1, 2) in chapter 2.7.3 are determined as follows
we find that the force and its Z-derivative acting on the conical part of the tip in accordance with formulas (1, 2) in chapter 2.7.3 are determined as follows
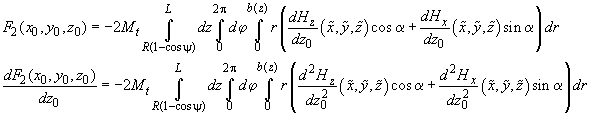
(9)
where 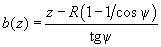 .
.
The total force and its derivative on this tip are then given by:
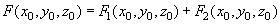
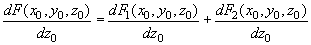
(10)






