2.7.10 Magnetic field of ring with current
Let us calculate the magnetic field generated by direct current
passing through a ring of radius
(Fig. 1). Let the width and thickness of a conductor be much less than
.
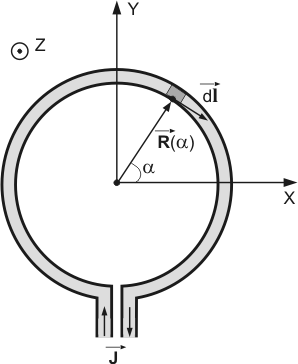
Fig. 1. Schematics of ring with current.
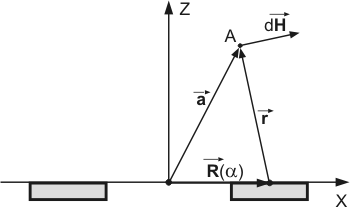
Fig. 2. Cross-section of the ring.
According to the Biot-Savart-Laplace law [1,2], the magnetic field produced by a current-carrying wire element of length
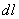at distance
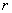from it in Gaussian coordinates is given by
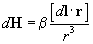
(1)
where
,
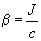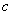– light velocity.
Placing the right-hand coordinate system XYZ into the ring center so that the XY plane lies in the ring plane (Fig. 1, 2) and noting that the problem is symmetrical relative to the ring center, it is enough to determine the magnetic field distribution in a plane containing vector codirectional with the ring radius and the Z-axis. For mathematical convenience we can choose the plane XZ and determine the magnetic field at point
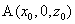as shown in Fig. 2. The radius-vector
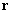from point
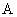to the ring element
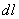as a function of angle
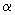is given by the following expression
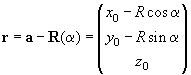
(2)
Elementary vector
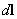as a function of
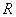and angle
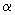is written as follows:
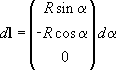
(3)
Substituting expressions (2) and (3) into formula (1), we get
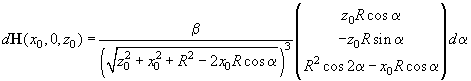
(4)
To determine the total magnetic field produced by all the ring at point
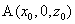, one needs to integrate every component of vector
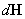with respect to
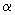from 0 to 2p. Then, the components X, Y and Z of vector
in accordance with (4) are defined as:
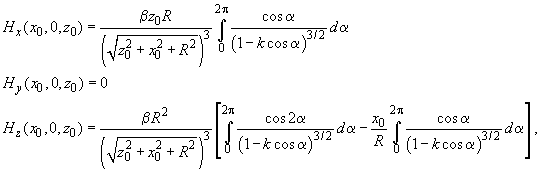
(5)
where
.
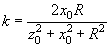Formulas (5) give the magnetic field distribution in the XZ plane. It is clear that due to the problem symmetry, the magnetic field along the Y-axis is zero and at an arbitrary point
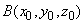it is equal to that at point
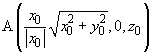in the XZ-plane. Accordingly, formulas (5) are rewritten as:
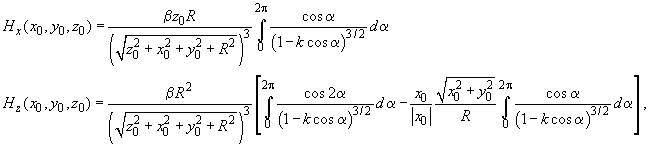
(6)
where
.
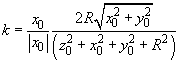Because
behaves as a parameter in the integrand of functions
and
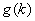, the first and second Z-derivatives of the magnetic field components can be obtained by direct differentiation of functions
,
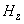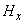with respect to
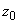and subsequent numerical integration. For example, the first
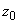-derivative of
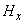in accordance with (6) is given by:
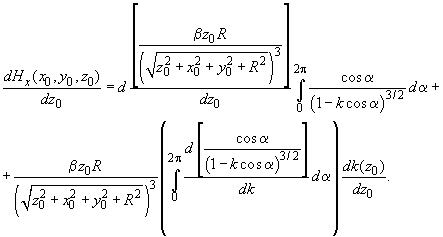
(7)
The other components of vector
are calculated similarly. In case
,
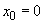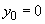(point
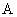is on the ring axis) formulas (6,7) are transformed as follows
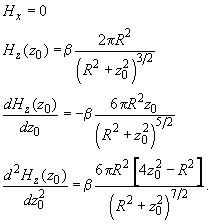
(8)
Using analitical expressions of the magnetic field first and second Z-derivates, one can calculate the interaction force (and its first derivative) between magnet probe and rectangular conductor with current. These calculations for different probe geometry are given in Appendix.
Summary.
- Derived are formulas (6-8) for the spatial distribution of the magnetic field and its derivatives along the Z-axis over a current ring.
References.
- D.V. Sivukhin. Electricity (General course of physics). Moscow, Nauka 1983. - 688 pp. (in Russian).
- R. Feinman, R. Leitos, M. Sands The Feinman lectures on physics. Electricity and magnetism. Moscow, MIR 1977. - 299 pp.