2.3.4 Cantilever small oscillations in a force field
Consider the case when in addition to the driving force (see (1) in chapter 2.3.3), an external force
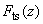 acts on an oscillator. The equation of motion in this case is written as
acts on an oscillator. The equation of motion in this case is written as
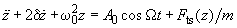
(1)
Because
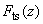 depends only on spatial coordinates, the qualitative feature of oscillations is the same as in (6) chapter 2.3.3. Force
depends only on spatial coordinates, the qualitative feature of oscillations is the same as in (6) chapter 2.3.3. Force
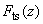 action results in the change of the oscillator equilibrium position about which the oscillations occur. For small oscillations we can take Taylor of
action results in the change of the oscillator equilibrium position about which the oscillations occur. For small oscillations we can take Taylor of
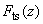 at point
at point
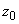 corresponding to the equilibrium position:
corresponding to the equilibrium position:
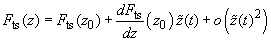
(2)
where
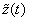 is expressed through
is expressed through
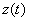 and
and
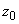 as follows:
as follows:
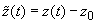
(3)
and 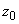 is determined from the following condition
is determined from the following condition
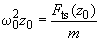
(4)
Changing
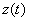 in equation (1) by
in equation (1) by
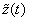 in accordance with (3) and taking into account (4), we get
in accordance with (3) and taking into account (4), we get
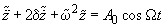
(5)
where
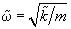 ,
,
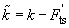 ,
,
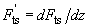 ,
,
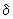 – damping factor determined in chapter 2.3.2.
– damping factor determined in chapter 2.3.2.
As can be seen, equation (5) is identical to (5) in chapter 2.3.3. These equations differ in 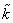 the introduction of the other spring stiffness
and new equilibrium position
the introduction of the other spring stiffness
and new equilibrium position
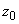 . Note that we can neglect the second order and higher terms in equation (2) only if the following condition is met
. Note that we can neglect the second order and higher terms in equation (2) only if the following condition is met
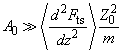
(6)
where
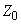 – oscillations amplitude at frequency
– oscillations amplitude at frequency
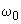 determined by formula (7) below. However, there are cases when
determined by formula (7) below. However, there are cases when
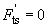 and the higher order terms in (2) are to be taken into consideration.
and the higher order terms in (2) are to be taken into consideration.
Similarly to formulas (7, 8) in chapter 2.3.3 and (8) in chapter 2.3.2, oscillations amplitude
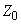 and phase shift
and phase shift
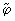 in the presence of external forces gradient is given by
in the presence of external forces gradient is given by
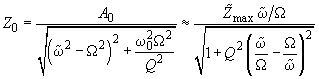
(7)
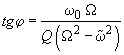
(8)
where
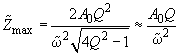 – oscillations amplitude at resonant frequency
– oscillations amplitude at resonant frequency
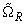 .
.
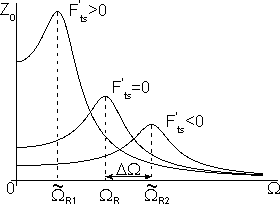
Thus, the force gradient results in an additional shift of a vibrating system amplitude-frequency characteristic (AFC) and phase-frequency characteristic (PFC). Fig. 1 shows AFC and PFC at different values of
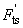 .
.
a)
b)
 .
.
Resonant frequency
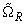 in the presence of external force can be written, by analogy with formula (10) in chapter 2.3.3, as
in the presence of external force can be written, by analogy with formula (10) in chapter 2.3.3, as
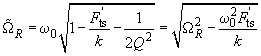
(9)
Hence, the additional shift of the AFC is

(10)
If
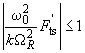 we can take Taylor of the radicand in formula (10) to obtain:
we can take Taylor of the radicand in formula (10) to obtain:
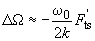
(11)
From expression (8) it follows that the force gradient results in the PFC shift so that its inflection point, at which the phase value is
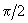 , corresponds to the frequency
, corresponds to the frequency
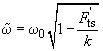
(12)
and
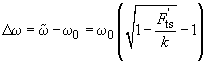
(13)
If condition
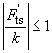 is met, formula (13) is the same as formula (11).
is met, formula (13) is the same as formula (11).
Let us determine the phase shift
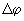 if there is force gradient present. If oscillations occur under the driving force at frequency
if there is force gradient present. If oscillations occur under the driving force at frequency
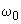 , the phase shift is
, the phase shift is
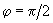 . In case of the force gradient presence, the phase shift in accordance with (8) becomes:
. In case of the force gradient presence, the phase shift in accordance with (8) becomes:
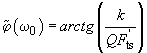
(14)
If
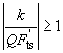 we can make a Taylor's expansion of expression (14) as follows
we can make a Taylor's expansion of expression (14) as follows
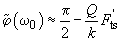
(15)
Hence, the additional phase shift due to the force gradient is (Fig. 2)
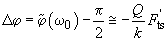
(16)
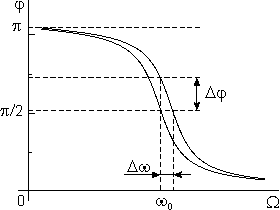
Fig. 2. Variation of the oscillations phase
with resonant frequency.
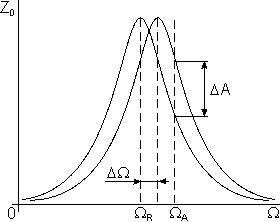
Fig. 3. Variation of the oscillations amplitude
with resonant frequency.
Consider now the amplitude change under the force gradient (Fig. 3).
The maximal change of
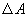 in case of the resonant frequency (9) variation, takes place at certain frequencies
in case of the resonant frequency (9) variation, takes place at certain frequencies
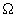 of the driving force. To these frequencies corresponds the maximum slope of the tangent to the AFC curve (linear portion of AFC):
of the driving force. To these frequencies corresponds the maximum slope of the tangent to the AFC curve (linear portion of AFC):
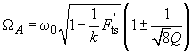
(17)
The change in oscillations amplitude (7) at frequency
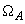 (Fig. 3) due to the force gradient in accordance with formulas (7) and (11) is given by
(Fig. 3) due to the force gradient in accordance with formulas (7) and (11) is given by
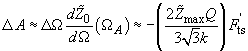
(18)
The considered oscillations mode is widely used in AFM. To study the force interaction of an oscillating cantilever with a sample, in particular, one can examine the change in resonant frequency (11), amplitude (18) and phase (16) of oscillations and then, according to obtained data, render the force
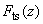 value (see, for example, chapter 2.7.1).
value (see, for example, chapter 2.7.1).
Summary.
- External force
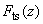 action (if condition (6) is met) results only in the change of the oscillator effective stiffness (resonant frequency) and equilibrium position about which the oscillations occur.
action (if condition (6) is met) results only in the change of the oscillator effective stiffness (resonant frequency) and equilibrium position about which the oscillations occur. - The system oscillations obey the law which is the same as in the absence of the external force.
- The change in resonant frequency, phase and amplitude of oscillations is proportional to the external force gradient and is determined by formulas (11), (16), (18).






