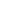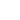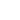2.3 Linear Oscillations of Cantilever
Study of a cantilever oscillation is a rather science – intensive problem. In many cases the general solution to the cantilever equation of motion can not be obtained in an analytical form. However, if cantilever deflections from the equilibrium position are small, oscillations of the system will be described by well known theories.
In chapter 2.1.1 it is shown that the Hooke's law properly describes the cantilever beam deflections from the equilibrium position. That is why small amplitude oscillations of the cantilever with one clamped end are qualified as oscillations of the spring pendulum having stiffness
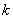 and some effective mass
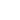
and some effective mass
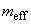 . The difference between the effective mass
. The difference between the effective mass
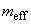 and the real cantilever mass is that not all cantilever oscillates with the same amplitude. The largest deflection takes place near the free end with a decay to zero at the clamped end. Chapter 2.1.6 presents calculations of the effective mass of the cantilever with given dimensions.
and the real cantilever mass is that not all cantilever oscillates with the same amplitude. The largest deflection takes place near the free end with a decay to zero at the clamped end. Chapter 2.1.6 presents calculations of the effective mass of the cantilever with given dimensions.
In this chapter we consider in detail problems of possible canti-lever linear oscillations modeling it as a spring pendulum. Oscillatory systems described by linear motion equation are called linear.