2.3.1 Natural oscillations
Consider the oscillating properties of the spring pendulum which is a point mass
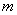 suspended from a motionless support by a massless spring having stiffness
suspended from a motionless support by a massless spring having stiffness
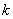 (Fig. 1).
(Fig. 1).

Fig. 1. Spring pendulum.
Let
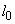 be the unstretched spring length. If mass
be the unstretched spring length. If mass
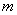 is attached to the spring, the latter will stretch due to gravity and its length will be
is attached to the spring, the latter will stretch due to gravity and its length will be
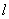 . If both the mass and the spring are in equilibrium (as shown in Fig. 1b) the gravity is balanced by elastic force
. If both the mass and the spring are in equilibrium (as shown in Fig. 1b) the gravity is balanced by elastic force
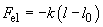 . Let the material point coordinate be the displacement of the mass from the equilibrium position
. Let the material point coordinate be the displacement of the mass from the equilibrium position
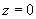 . Then the equation of motion can be written in the form [1-3]:
. Then the equation of motion can be written in the form [1-3]:
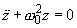
(1)
where
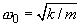 – frequency of natural undamped oscillations or the natural frequency. The cantilever eigenfrequency
– frequency of natural undamped oscillations or the natural frequency. The cantilever eigenfrequency
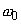 has been calculated in chapter 2.1.6.
has been calculated in chapter 2.1.6.
Solution of equation (1) with initial conditions
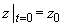 and
and
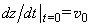 is given by
is given by
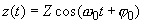
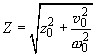
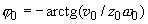
(2)
The amplitude and initial phase of free oscillations are determined by starting conditions for the coordinate and velocity while frequency of natural undamped oscillations is a parameter of an oscillating system.
The considered type of oscillations is usually called free oscillations because they occur in an oscillating system which is put out of balance and left alone.
Summary.
- Small cantilever oscillations are described by the oscillation law of the spring pendulum with given stiffness and effective mass.
- In case of external forces absence, natural oscillations are harmonic (2).
References.
- S.E. Hikin. Mechanics. – Moscow: OGIZ, 1947. – 574 pp. (in Russian)
- D.V. Sivukhin. Mechanics. – Moscow: Nauka, 1989. – 576 pp. (in Russian)
- Carlov N.V., Kirichenko N.A. Oscillations, waves, structures. – Moscow: PHYSMATLIT, 2003. – 496 pp. (in Russian)






