2.3.3 Oscillations in the presence of external periodic driving force
Ideal case.
Let the external periodic force act on a ball of the spring pendulum:
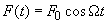
(1)
In this case the displacement of the ball from its equilibrium position is defined instead of equation (2) in chapter 2.3.2 by the following equation:
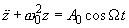
(2)
where 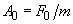 .
.
The solution of equation (1) at
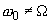 is easily written down as [1-3]:
is easily written down as [1-3]:
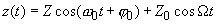
(3)
where
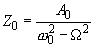
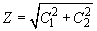
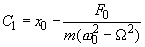
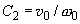
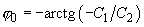
The first summand in (3) describes free oscillations while the second – the so called forced oscillations with amplitude
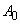 . Thus, if a driving force is acting, the amplitude and the initial phase of oscillations depend not only on initial conditions but on the force parameters.
. Thus, if a driving force is acting, the amplitude and the initial phase of oscillations depend not only on initial conditions but on the force parameters.
In an extreme case of frequencies
 and
and
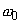 coincidence, the system can not experience a periodic oscillation. The coordinate
coincidence, the system can not experience a periodic oscillation. The coordinate
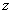 evolution in time will be described by the following formula:
evolution in time will be described by the following formula:
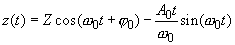
(4)
Such motion can be considered as an oscillation whose amplitude increases linearly with time. The phenomenon of oscillations amplitude unlimited growth under the periodic external force is called the resonance phenomenon.
It should be emphasized that the resonance growth of the forced oscillations amplitude beyond all bounds is an idealization of the system. Firstly, when oscillations amplitude becomes large enough, the oscillator, as a rule, is no longer the linear one. Secondly, while defining equation (12), the frictional forces which damp oscillations were not taken into consideration. Therefore, the last factor should be considered in more detail.
Forced oscillations in the presence of friction.
If driving force (1) acts on an oscillator with friction, the equation of motion is written as:
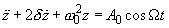
(5)
where
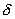 – damping factor defined in chapter 2.3.2.
– damping factor defined in chapter 2.3.2.
A general solution of (5) reads [1–3]
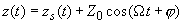
(6)
where
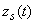 – equation (5) solution in the absence of external force (oscillator natural damped oscillations (3) – (5) in chapter 2.3.2.
– equation (5) solution in the absence of external force (oscillator natural damped oscillations (3) – (5) in chapter 2.3.2.
Due to the friction, the condition
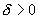 is met and natural oscillations are damped:
is met and natural oscillations are damped:
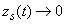 at
at
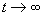 . Therefore, over the time
. Therefore, over the time
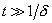 only forced oscillations will present in the system which are described by the second summand in (6). It is important to realize that parameters of forced oscillations are independent on starting conditions. Parameters of these oscillations: frequency is equal to the driving force frequency
only forced oscillations will present in the system which are described by the second summand in (6). It is important to realize that parameters of forced oscillations are independent on starting conditions. Parameters of these oscillations: frequency is equal to the driving force frequency
 , amplitude is
, amplitude is
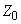 and
and
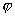 phase shift is :
phase shift is :
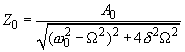
(7)
(8)
As it arises from formula (8), factor
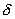 depends on the function
depends on the function
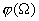 derivative in the following way:
derivative in the following way:
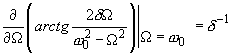
(9)
The case under study differs from the case of the forced oscillator without friction in the phase shift
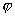 between driving force and oscillations. If the forcing frequency is equal to the natural frequency, i.e.
between driving force and oscillations. If the forcing frequency is equal to the natural frequency, i.e.
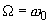 , the phase shift is
, the phase shift is
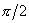 independently on the degree of damping.
independently on the degree of damping.
Another sufficient consequence of damping is the qualitative change in the resonance curve shape. Fig. 1 shows relations 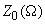 and
and
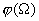 for some characteristic values of
for some characteristic values of
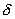 .
.
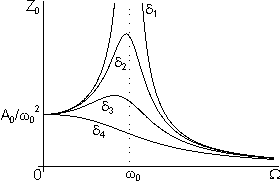
Fig. 1a. Resonance curves (AFC) of the linear oscillator for different values of the friction coefficient:
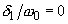 ,
,
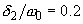 ,
,
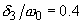 ,
,
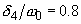 .
.
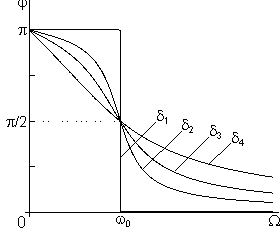
Fig. 1b. Phase
 shift between driving force and oscillations depending on driving frequency (PFC).
shift between driving force and oscillations depending on driving frequency (PFC).
The upper bound of forced oscillations amplitude (7) is given by
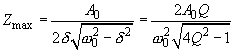
(10)
The corresponding resonance frequency amounts to:
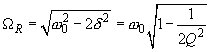
(11)
on the assumption of
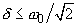 . In case of light damping (
. In case of light damping (
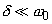 ) the resonance frequency is approximately equal to the oscillator natural frequency
) the resonance frequency is approximately equal to the oscillator natural frequency
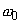 . As
. As
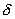 increases, this frequency shifts to lower values (see Fig. 1 a). At
increases, this frequency shifts to lower values (see Fig. 1 a). At
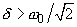 , the maximum of the forced oscillations amplitude
, the maximum of the forced oscillations amplitude
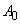 corresponds to the frequency
corresponds to the frequency
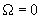 . This in fact means that the resonance vanishes. Previously it was pointed out that the regime of free oscillations aperiodic damping takes place only if
. This in fact means that the resonance vanishes. Previously it was pointed out that the regime of free oscillations aperiodic damping takes place only if
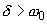 . Hence, in the range
. Hence, in the range
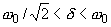 , the forced oscillations are no longer of the resonant character while the oscillator motion is still oscillatory.
, the forced oscillations are no longer of the resonant character while the oscillator motion is still oscillatory.
As it is seen from formula (7), for light damping
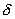 , the forced oscillations amplitude decays rapidly as frequency goes far from the resonance one. In particular, it decreases
, the forced oscillations amplitude decays rapidly as frequency goes far from the resonance one. In particular, it decreases
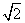 times at the following
times at the following
 values:
values:
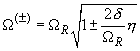 ,
,
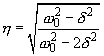
(12)
The quantity
 is called the resonant width. At small
is called the resonant width. At small
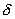 its magnitude is
its magnitude is
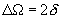 . Then the quality factor defined by formula (8) in chapter 2.3.2 is related to the resonant width as:
. Then the quality factor defined by formula (8) in chapter 2.3.2 is related to the resonant width as:
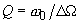
(13)
Thus, the resonant width is determined by the quality factor and the natural frequency. The more is the oscillating system quality factor, the less is the resonance peak width. As follows from formula (13), the oscillatory system Q-factor as well as the damping factor can be estimated from experimental amplitude-frequency characteristic (AFC) of an oscillator.
Summary.
- Oscillations of forced oscillatory system are described by periodic function, the amplitude and initial phase of oscillations being dependent not only on the starting conditions but on the driving force (3) parameters.
- If forcing frequency
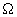 and natural frequency
and natural frequency
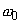 are the same, the system oscillations amplitude (4) gradually increases, i.e. the resonance phenomenon occurs.
are the same, the system oscillations amplitude (4) gradually increases, i.e. the resonance phenomenon occurs. - In case of forced oscillating system with friction, only forced oscillations described by the second term in (6) will exist in the system after time
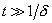 .
. - Parameters of the forced oscillation do not depend on initial conditions. These oscillations have the frequency of driving force
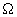 and are characterized by amplitude (7) and phase shift (8). If frequencies coincide, i.e.
and are characterized by amplitude (7) and phase shift (8). If frequencies coincide, i.e.
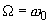 , the phase shift is equal to
, the phase shift is equal to
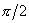 independently on the degree of damping.
independently on the degree of damping. - The resonant width is determined by the quality factor and the natural frequency (13).
References.
- S.E. Hikin. Mechanics. – Moscow: OGIZ, 1947. – 574 pp. (in Russian)
- D.V. Sivukhin. Mechanics. – Moscow: Nauka, 1989. – 576 pp. (in Russian)
- Carlov N.V., Kirichenko N.A. Oscillations, waves, structures. – Moscow: PHYSMATLIT, 2003. – 496 pp. (in Russian)






