2.3.2 Oscillations in the presence of friction
In chapter 2.3.1 natural oscillations of the cantilever in the absence of external forces are considered. In real systems there always takes place the dissipation of energy. If energy losses are not compensated outside, the oscillation will damp in time and eventually stop. Let us consider the spring pendulum oscillations in a viscous medium.
The frictional force acting on a body moving in a homogeneous viscous media depends only on the velocity. At small velocities the frictional force can be approximated as:
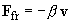
(1)
where
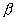 – constant positive factor.
– constant positive factor.
Taking into account the frictional force (1), the motion equation of the spring pendulum instead of (1) in chapter 2.3.1 will be written as [1-3]:
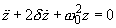
(2)
where
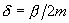 – damping factor.
– damping factor.
There are three types of the equation (2) solution:
- If
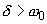 (case of large resistance), the solution to equation (2) is given by
where independent constants
(case of large resistance), the solution to equation (2) is given by
where independent constants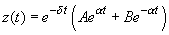
(3)
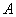 and
and
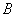 are determined from initial conditions. As can be seen, in this case oscillations do not occur. Such motion regime is called the aperiodic.
are determined from initial conditions. As can be seen, in this case oscillations do not occur. Such motion regime is called the aperiodic.
- If
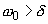 , the solution to equation (2) is written as:
, the solution to equation (2) is written as:
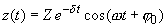
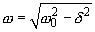
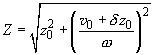
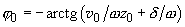
(4)
In this case, the character of oscillations in the presence of the frictional force is described by a periodic function with exponentially decreasing amplitude.
-
In case
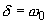 , a critical damping takes place. Equation (2) solution reads:
where independent constants
, a critical damping takes place. Equation (2) solution reads:
where independent constants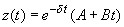
(5)
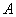 and
and
 are determined as before by initial conditions.
are determined as before by initial conditions.
Fig. 1 shows the plot of the oscillation amplitude vs. time for different ratios between parameters
 and
and
 .
.
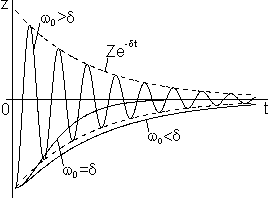
Fig. 1. Dependence for different ratios between natural frequency
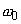
and damping factor
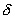 .
.
Frequently, the "quality" of an oscillatory system is characterized by dimensionless parameter
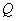 called the quality- or Q-factor. It is proportional to the ratio between stored energy
called the quality- or Q-factor. It is proportional to the ratio between stored energy
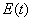 and energy loss over the period
and energy loss over the period
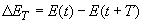 [3]:
[3]:
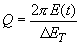
(6)
In case of small damping (
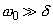 ) the total energy as a function of time is:
) the total energy as a function of time is:
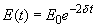
(7)
where
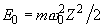 – initial magnitude of the oscillator total energy. Then, in accordance with formulas (6) and (7)
– initial magnitude of the oscillator total energy. Then, in accordance with formulas (6) and (7)
Thus, the Q-factor characterizes the rate of the energy transformation in a system. On the other hand, by the order of magnitude the quality factor is nothing but the number of a system oscillations over its characteristic damping time . Notice that the Q-factor not only defines the oscillations damping but is also an important quantity that determines parameters of forced oscillations under external periodic force (see chapter 2.3.3).
Summary.
- In the presence of a frictional force, the type of natural oscillations is determined by the ratio between
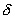 and
and 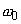 . At
. At
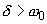 aperiodic regime (3) takes place; at
aperiodic regime (3) takes place; at
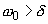 oscillations are periodic with exponentially decreasing amplitude (4); at
oscillations are periodic with exponentially decreasing amplitude (4); at
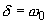 the regime of critical damping (5) exists.
the regime of critical damping (5) exists. - The quality factor of an oscillating system is a very important parameter characterizing dissipative processes in a system.
References.
- S.E. Hikin. Mechanics. – Moscow: OGIZ, 1947. – 574 pp. (in Russian)
- D.V. Sivukhin. Mechanics. – Moscow: Nauka, 1989. – 576 pp. (in Russian)
- Carlov N.V., Kirichenko N.A. Oscillations, waves, structures. – Moscow: PHYSMATLIT, 2003. – 496 pp. (in Russian)






