2.7.2 Algorithms for the physical parameters of the sample obtaining
What information about the sample magnetic properties can we reveal knowing the derivative of the magnetic interaction force with respect to vertical direction  ?
?
- Spatial periodicity and domain structure dimensions. Qualitative analysis.
To get the sample qualitative picture and observe its magnetic properties (for example, spatial periodic domain structure), there often is enough to know the derivative of magnetic interaction force. It is clear that the detected force of magnetic interaction and field are actually constant as tip moves over domain. When the cantilever passes across a domain wall, a smoothed step of the resonance oscillation phase and amplitude is observed which corresponds to the force change. This is, in fact, the only picture we can obtain for the sample with a rather coarse magnetic structure.
- Quantitative analysis (classical approach).
To quantify the experimental data, the chart shown in Fig. 1 is normally employed.
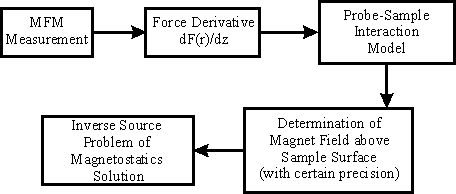
Fig. 1. MFM results processing chart.
First, the
 value is calculated in accordance with expressions (2)–(4) of chapter 2.7.1 using experimental results. Next, the magnetic field is rendered in the tip vicinity. To do that we need to choose a physical model that describes the magnetic probe interaction with external magnetic field. Depending on the probe used, these models can be classified as follows [1]:
value is calculated in accordance with expressions (2)–(4) of chapter 2.7.1 using experimental results. Next, the magnetic field is rendered in the tip vicinity. To do that we need to choose a physical model that describes the magnetic probe interaction with external magnetic field. Depending on the probe used, these models can be classified as follows [1]:- Hard magnetic cantilever.
- General expression of the interaction force between a magnetic cantilever and a sample (see chapter 2.7.3).
- Point dipole approximation (see chapter 2.7.4).
- Point monopole approximation (see chapter 2.7.5).
- Soft magnetic cantilever.
- Paramagnetic cantilever
Thus, having chosen one of the mentioned models, one can render the magnetic field distribution in space above a sample. Notice that regardless of the model chosen, the magnetic field map will be rendered to some accuracy because firstly, the probe oscillation amplitude is considered theoretically to be infinite small as compared to probe-sample separation. In practice, this condition is almost never satisfied so the amplitude finitness must be taken into consideration. In other words, in MFM,
 is measured not locally but in some tip vicinity dependent on its oscillation amplitude. Experimental magnitude of
is measured not locally but in some tip vicinity dependent on its oscillation amplitude. Experimental magnitude of
 is in fact the averaged value in this vicinity. Secondly, the finitness of the tip-sample interaction region is to be taken into consideration, too.
is in fact the averaged value in this vicinity. Secondly, the finitness of the tip-sample interaction region is to be taken into consideration, too.
The last step of the chart (Fig.1) is the sample magnetic structure representation. To determine the studied surface magnetization (distribution of unit volume magnetic moment), the so called inverse source problem of magnetostatics should be solved. Remember that the forward problem is the field calculation from the known sources while the inverse problem is the sources positions determination basing on the information about the field structure. Thus, the inverse problem solution means determination of magnetization distribution across the sample surface under given magnetic field distribution in space. Because the field distribution has been previously rendered to some accuracy, the magnetization distribution will be rendered with a gross error. Moreover, in some cases the inverse problem can not be solved in principle. That's why another algorithm of MFM data quantitative interpretation is needed.
- Hard magnetic cantilever.
- Parametric method (alternative to classical approach)
To interpret quantitatively the experimental results, the following algorithm shown in Fig. 2 is proposed.
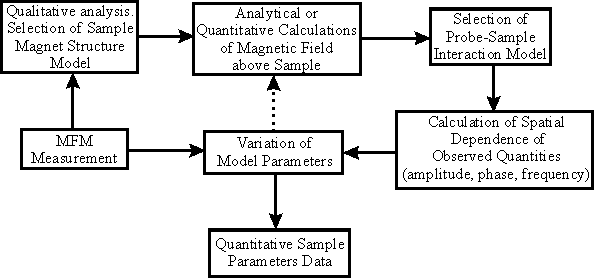
Fig. 2. Algorithmic diagram of MFM data analysis.
First, the qualitative analysis of the studied sample is performed. Then, the acquired qualitative relations are compared to theoretical ones obtained from model problems. Here it means that we can choose between various theoretical expressions for the derivative of the magnetic field force acting on the tip calculated for the most common magnetic structures. In particular, such database should contain as a minimum qualitative MFM results for the following magnetic structures: single magnetic bubble, periodic magnetic bubble pattern (with variation in size and magnetization orientation), chapter 2.7.11; single laminar domain, periodic pattern of laminar domains (with variation in size and magnetization orientation); periodic pattern of parallel domains, chapter 2.7.12, etc. Having compared experimental data with an image from the database, we can choose the sample configuration model that fits best.
Further, we select a model of the tip interaction with an external magnetic field (these models are mentioned above) and within the framework of this model compute variation in detected parameters (phase, amplitude, frequency) having set previously the problem initial parameters: probe geometry, probe magnetization, tip-sample separation. Then, by varying the model unknown parameters depicting the sample magnetic structure, achieve the best agreement between calculation and measurement. These unknown parameters that provide the agreement represent the quantitative data about the sample magnetic structure. Sometimes, limited experimental data restrict the determination of the model parameters uniquely with high accuracy. In this case, according to the analysis results it is possible to limit the range of allowable values of the model parameters.
Thus, to quantify the magnetic characteristics of the studied structures within the framework of this algorithm, it is necessary:
- to perform the qualitative MFM investigation of the sample structure.
- to choose the model of the magnetic field distribution in the sample.
- to choose the model of the probe interaction with the sample magnetic field.
- to adjust such unknown parameters of the sample magnetic field model that calculation and measurement agree well.
Summary.
- In this section the basic problems of MFM data interpretation are considered.
- Two algorithms of the MFM data analysis are theoretically examined.
- It is shown that to solve in principle the inverse problem of magnetostatics one should just choose the model of the probe interaction with the sample field and know magnetic characteristics of the probe. In practice, however, it is more efficient to use the parametric method of MFM data analysis.
References.
- P. Grutter, H.J. Mamin, D. Rugar, in Scanning Tunneling Microscopy II, edited by R. Wiesendanger and H.-J. Guntherodt (Springer, Berlin, 1992) pp. 151-207.






