2.6.7 Appendices
APPENDIX I.
In the early model of the microscope Solver P47 the cantilever axis is inclined 20° to the sample plane (Fig. 1). The plane of incident and reflected beams is perpendicular to the cantilever axis. The angle between these beams is 40°. The beam reflected off the non-deflected cantilever is perpendicular to the photodiode plane.
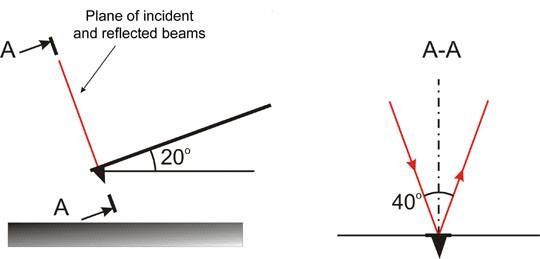
Fig. 1. Optical detection system orientation in space.
Omitting calculations, we present the angles value:
| angle, ° | cos | |
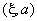 |
20 | 0.94 |
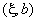 |
83.3 | 0.12 |
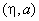 |
90 | 0 |
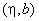 |
20 | 0.94 |
APPENDIX II.
Given below is an example of the calibration constant calculation (LAT signal vs. lateral force) for the early model of the Solver P47 microscope having silicon cantilever CSC12 with the following characteristics:
| length | l = 90 mm |
| tip height | 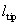 = 10 mm = 10 mm |
| spring constant | 1/c = 0.52 N/m |
Experimental plots of the DFL and LAT signals vs. adjusting screws travel x and h are shown in Fig. 2.
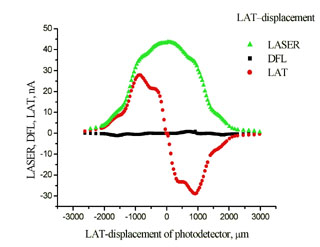
Fig. 2a. Experimental plots
DFL(x), LAT(x).
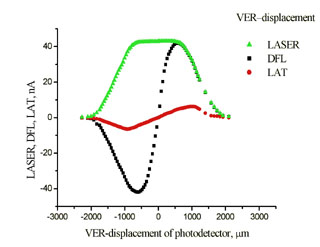
Fig. 2b. Experimental plots
DFL(h), LAT(h).
The laser spot on the photodetector is of irregular shape and has irregular intensity. As a result, obtained relations differ from the ideal ones (see Fig. 5 chapter 2.6.3). The uneven curve in Fig. 2b is the evidence of the spot intensity side maximums arising apparently from the light diffraction. The reason for the lack of plateau on plots is the spot diameter exceeding half the photodetector size. To determine the B constant, the linear portion of the plot LAT(x) in Fig. 2a and data from Appendix I are used.
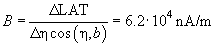
Substituting values into expression (2) chapter 2.6.4, we get
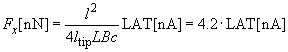
APPENDIX III.
Problem.
Determine the interaction potential of a polyatomic tip with a surface within the model of the pairwise Van der Waals interaction of individual molecules.
Solution.
The potential of two atoms interaction (neutral atoms having no dipole moment) at large (relative to the atom size) separation is given by
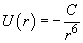
(1)
where
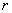 – separation between atoms,
– separation between atoms,
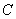 – constant of Van der Waals interaction which can be expressed through atoms polarizability.
– constant of Van der Waals interaction which can be expressed through atoms polarizability.
Consider potential
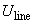 of interaction between an atomic chain of identical atoms separated by distance
of interaction between an atomic chain of identical atoms separated by distance
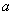 and a single atom at distance
and a single atom at distance
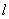 from the chain;
from the chain;
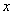 is the distance to the neighbor atom along the chain.
is the distance to the neighbor atom along the chain.
It is obvious that
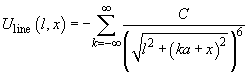
(2)
where
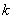 – atom number in chain.
– atom number in chain.
Normalizing lengths by period
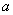 and introducing designations
and introducing designations
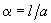 and
and
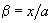 , we get
, we get
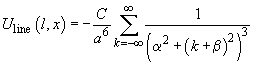
(3)
The sum in this expression can be calculated accurately which gives
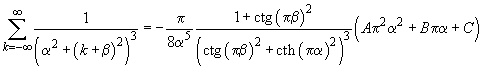
(4)
where
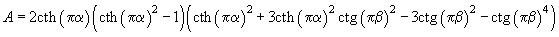
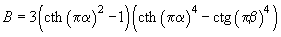
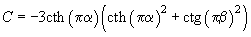
(5)
The sum calculation results for two different values of parameter
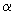 are shown in Fig. 1.
are shown in Fig. 1.
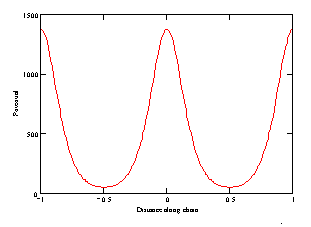
a)
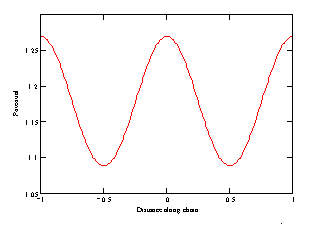
b)
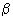 )
) at constant distance between atom and chain axis: (a)
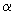 = 0.3, (b)
= 0.3, (b)
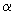 = 1.
= 1.
As seen from Fig. 1a, at small distance to the chain axis, the potential is of complicated form, but as the distance increases (Fig. 1b), the potential becomes sineshaped. Note that assuming the interatomic potential to be that for the Van der Waals interaction, we thereby supposed that the distance between atoms is more then atom size.
In extreme case of large values
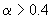 the sum can be approximated by following expression
the sum can be approximated by following expression
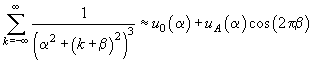
(6)
where
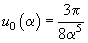 ,
,
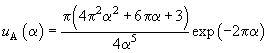 .
.
To obtain the potential of interaction with atomic plane one should sum the derived formula over all atomic chains on the surface properly changing parameter
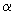 . However, calculation of such a sum in analytic form is impossible. Nevertheless, the mean value of potential can be easily obtained by reducing summation to integration and assuming that atomic density is "uniformly spread" over a sample volume.
. However, calculation of such a sum in analytic form is impossible. Nevertheless, the mean value of potential can be easily obtained by reducing summation to integration and assuming that atomic density is "uniformly spread" over a sample volume.
The oscillating term
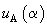 in the formula is responsible for the pseudoatomic resolution of scanning microscopy. Evidently, due to the exponential factor, the noticeable contribution into the interaction can give only neighbor atomic chains. As an example, consider [100] plane of a cubic lattice. The accurate calculation of the contribution of underlying layers into the potential for such a surface do not exceed 0.1%, therefore we shall restrict ourselves to considering only the top layer. Let
in the formula is responsible for the pseudoatomic resolution of scanning microscopy. Evidently, due to the exponential factor, the noticeable contribution into the interaction can give only neighbor atomic chains. As an example, consider [100] plane of a cubic lattice. The accurate calculation of the contribution of underlying layers into the potential for such a surface do not exceed 0.1%, therefore we shall restrict ourselves to considering only the top layer. Let
 be the dimensionless distance over the surface in
be the dimensionless distance over the surface in
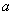 units and
units and
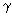 – dimensionless distance across the chain axis. Then, the potential of interaction with the surface is written as:
– dimensionless distance across the chain axis. Then, the potential of interaction with the surface is written as:
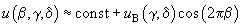
(7)
Taking into account three neighbor atomic chains, we get:
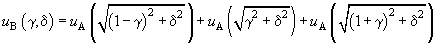
(8)
Considering only case of large
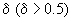 we can obtain a good approximation:
we can obtain a good approximation:
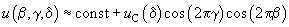
(9)
where 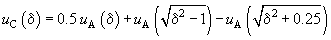 .
.
Returning to dimensional units, we can write:
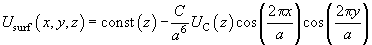
(10)
where 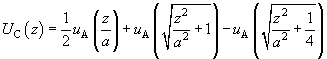 .
.
Result.
The oscillating part of the atom-surface interaction potential at the distance of the order of atomic period and more is the periodic function (cosine) with the period of atomic lattice (for the [100] plane of cubic lattice).
Note.
For the other lattice types, e.g. graphite, the contribution of underlying layers can be considerable, therefore, the period in the image can be less than the interatomic distance in the top layer.






