2.6.5 Stick-slip motion on the nanoscale
Introduction.
The nanotribology aim is explanation and modeling of friction on the atomic scale. In contrast to microtribology which operates with notions and terminology of the continuum theory, nanotribology utilizes more fundamental concepts based on individual atoms interaction.
The most available tool for experiments in nanotribology is the atomic force microscope. The probe's tip permits to "sense" friction on a tiny contact area of only few atoms.
Our goal is the construction of the model of friction between a tip and a sample on the nanoscale. We have to describe a cantilever motion and find the frictional force the surface exerts on it at scan. The built-in program allows to carry out numerical calculations and change the model parameters at your discretion.
Cantilever modeling.
A cantilever (or, rather, its tip) is simulated by a linear two-dimensional damped oscillator that can vibrate only in the horizontal plane Oxy. The oscillator is described by six characteristics:
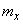 ,
,
 – effective masses for oscillations in corresponding directions,
– effective masses for oscillations in corresponding directions,
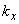 ,
,
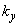 – stiffness,
– stiffness,
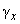 ,
,
 – damping factors along x and y axes.
– damping factors along x and y axes.
Tip vertical move is not considered in this model so the z-components of cantilever characteristics are not used in calculations.
Sample surface modeling.
The distribution of Van der Waals potential of the sample lattice surface (interatomic distance
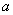 ) at height
) at height
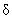 over it is of a periodic character. Potential of a single chain can be calculated precisely (see Appendix III). Far enough from the surface
over it is of a periodic character. Potential of a single chain can be calculated precisely (see Appendix III). Far enough from the surface
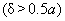 , this function can be approximated by the sine function with the period of the sample lattice.
, this function can be approximated by the sine function with the period of the sample lattice.
Basing on the calculated Van der Waals potential which determines the interaction energy of a separate ("point-like") atom with a sample, one can find the interaction potential of the whole tip with the surface by summation the obtained in the Appendix function over all the tip atoms. This two-dimensional distribution of the potential of the tip positioned over a given surface point describes the sample in our model. This potential also has the periodic structure reflecting the sample lattice. Note, that one should not confuse this distribution for interaction with an extended object with a usual atomic lattice potential which describes the energy of sample atoms interaction with a point-like particle. In our case, this is the potential of interaction with the whole tip.
The function character depends on the tip curvature radius. The more the radius is, the more smooth is the potential distribution. For quite dull tips (of the order of 100 nm) the function periodic structure disappears. In this case our model is not applied and microtribology should be addressed.
As it follows from calculations in the Appendix III (where the Van der Waals potential of a single atom depends on its height over the surface
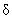 ), the tip potential depends not only on horizontal coordinates but on the vertical coordinate
), the tip potential depends not only on horizontal coordinates but on the vertical coordinate
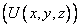 , i.e. on the tip height over the surface. Because scanning occurs at constant height
, i.e. on the tip height over the surface. Because scanning occurs at constant height
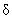 , the vertical coordinate contribution is taken into account through potential amplitude
, the vertical coordinate contribution is taken into account through potential amplitude
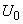 . Not going into details, the potential distributions for highly oriented pyrolytic graphite (HOPG) and molybdenite
. Not going into details, the potential distributions for highly oriented pyrolytic graphite (HOPG) and molybdenite
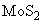 will be approximated by following functions [1,2]:
will be approximated by following functions [1,2]:
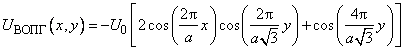
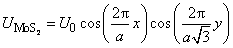
(1)
where
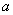 – lattice period. For HOPG the lattice period is 2.46 nm, for molybdenite
– lattice period. For HOPG the lattice period is 2.46 nm, for molybdenite
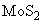 – 3.16 nm.
– 3.16 nm.
One-dimensional model.
For qualitative understanding of the nanofriction model we shall consider, first, the one-dimensional model of probe oscillations in one direction along the Ox-axis. Potential (1) in this case is reduced (by eliminating non-principal constants) to the following
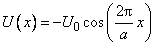
(2)
where
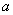 – lattice period.
– lattice period.
Let cantilever of mass
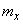 attached to an elastic suspension of stiffness
attached to an elastic suspension of stiffness
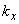 move in potential
move in potential
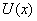 , a carriage being moved with constant velocity
, a carriage being moved with constant velocity
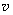 . The model is described by the following equation [1]:
. The model is described by the following equation [1]:
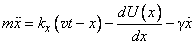
(3)
The resulted motion character is depicted in Fig. 1 as a plot
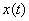 . When moving "uphill", the probe experiences negative force from the sample and the spring stretches. Upon reaching the "peak", the probe jumps off and starts to oscillate with damping.
. When moving "uphill", the probe experiences negative force from the sample and the spring stretches. Upon reaching the "peak", the probe jumps off and starts to oscillate with damping.
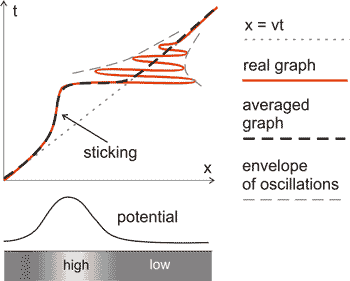
Fig. 1. The probe stick-slip motion in the one-dimensional model.
If oscillations are averaged (as shown in Fig. 1 with a dotted line), the jogging motion or the so called "stick-slip" is clearly seen. The frictional force in this case is of the saw-tooth character.
Two-dimensional model.
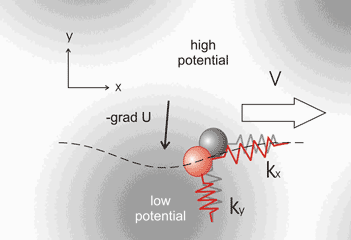
Fig. 2. In the two-dimensional model the probe can deflect laterally.
A possible situation in the absence of potential is shown in gray.
Actual probe position is shown in red.
It is easy to obtain the two-dimensional generalization of the above model (Fig. 2). The following formulas can be written for the case of line
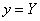 scan in the Ox direction with speed
scan in the Ox direction with speed
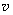 [3]:
[3]:
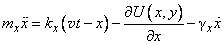
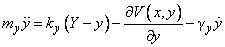
(4)
For the two-dimensional case, the motion has some features. The probe moves not only in the scan direction but from side to side in the Oy direction because the tip "slithers" down the potential humps sideways approaching the energy minimum.

Fig. 3. During scanning the probe moves not only laterally turning round obstacles, but "sticks" ascending the potential maximums. Dotted line shows scan direction, red points correspond to the probe position in equal intervals.
In Fig. 3 dots show a possible trajectory of the tip move. The time interval between dots is the same so one can see that at sites of potential minimum when the probe has to go "uphill" it is delayed while the "downhill" is passed rapidly.
Simplification of calculations.
The direct use of formulas (4) in calculations requires large enough computer power. For computation of fast and strongly damped (damping of the order of 103) cantilever oscillations it is necessary to use small enough integration time step, so calculations delay.
Within the scope of this model we do not need to reveal details of an oscillation process. It is just enough to trace the tip position averaged over a few periods and not to trace oscillations until total attenuation which is time and resource consuming. If we neglect the second derivative in equations (4), calculations can be noticeably accelerated, the stick-slip behavior being preserved.
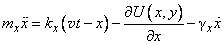
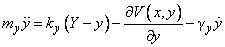
(5)
The built-in program features.
In the built-in program (see Flash model) the simplified set of equations (5) without the second derivative (or with zero mass which is the same). You can choose:
- model parameters ("Show problem" button)
- one of two sample materials (highly oriented pyrographite or molybdenite
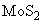 )
) - fast scan direction (along or across the cantilever axis)
- scanning speed (
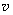 )
) - cantilever orientation relative to the sample ("scan angle")
- calculation (not scan!) scheme: only "forth" or "back and forth". (In the second case the running time is double but an image quality at edges is improved due to the lack of an arbitrariness in choosing boundary conditions in every scan line)
- one of two sample materials (highly oriented pyrographite or molybdenite
- cantilever parameters
- it is possible to choose between one of the standard cantilevers and "My" cantilever typing dimensions of the latter
- cantilever stiffness (
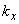 ,
,
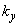 ) along axes being calculated automatically in accordance with formulas (7) in chapter 2.1.4 and (10) in chapter 2.1.3
) along axes being calculated automatically in accordance with formulas (7) in chapter 2.1.4 and (10) in chapter 2.1.3
- computation parameters
- studied area dimensions
- number of points along axes
To consider properly the stick-slip motion (and, accordingly, calculate correctly the atomic structure) it is necessary to set more than 30 points of calculation grid per lattice period. This number of points per period is desirable to be integer for obtaining image details. To calculate (and set up) this number, one should know lattice period
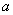 , scan size (along fast scan axis)
, scan size (along fast scan axis)
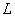 , points number in line
, points number in line
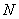 . Then, number of points per period is
. Then, number of points per period is
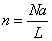 .
.
We have to mention how parameters that do not appear in formulas are applied. Setting a sample orientation means the turn of function (2) in plane Oxy by changing of variables using the rotation matrix:
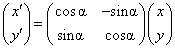
(6)
where
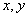 – old coordinates,
– old coordinates,
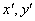 – new coordinates,
– new coordinates,
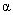 – rotation angle.
– rotation angle.
Considering results.
The built-in program (see Flash model) allows to depict with shades of grey the deflections of the probe from the non-deformed position along Ox and Oy axes – signals LAT and DFL, respectively. The user can choose any signal distribution to display from the drop-down menu in the top right corner upon calculation completion.
The obtained picture exhibits the periodic behavior corresponding to the lattice period, however maximums of the frictional force are shifted relative to the potential peaks distribution.
From the image one can easily determine the scan direction. Step transitions from light to dark shades correspond to the probe slips after sticking. As the scan speed increases, the contrast of transitions is lowered.
How to obtain a clear atomic structure image?
How clear is the structure of an atomic lattice being imaged depends sufficiently on the scan direction. Fig. 4 shows schematically the probe trajectory when scanning along (a) and across (b) atoms chain. As follows from the model, the sticking occurs at lattice points and the probe "slithers" down into these potential minimums (see above "Two-dimensional model").
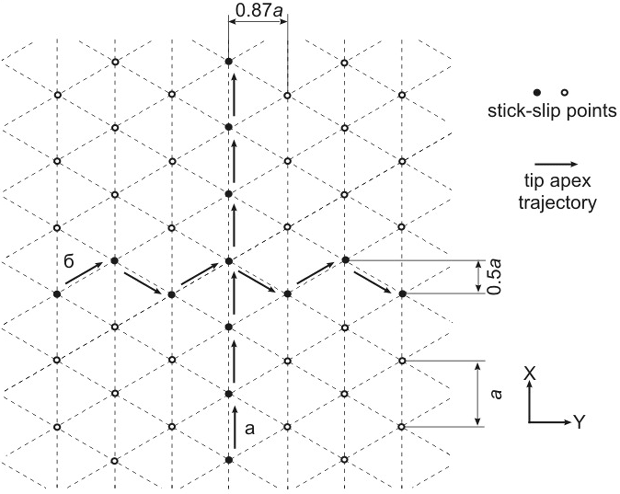
Fig. 4. Probe trajectory during scanning along (a) and across (b) atomic chains.
In case (а) the deflection in the Oy direction (across the scan direction) is absent that results in no atomic resolution in the respective signal (LAT or DFL depending on cantilever orientation). Information about the structure will carry only the signal of deflection along Ox which will exhibit the saw-tooth profile or stick-slip behavior.
On the other hand, the atomic resolution in line (b) follows from the deflection signal registered in both Oy and Ox directions. The first of the signals is of the zig-zag form while the second resembles the square-sine function with period
 because the probe sticks either to the right or to the left from the scan line.
because the probe sticks either to the right or to the left from the scan line.
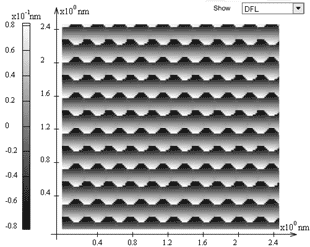
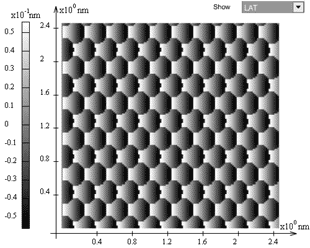
Fig. 5. (a) – cantilever and fast scan axis orientations relative to the lattice;
(b) – DFL signal distribution; (c) – LAT signal distribution.
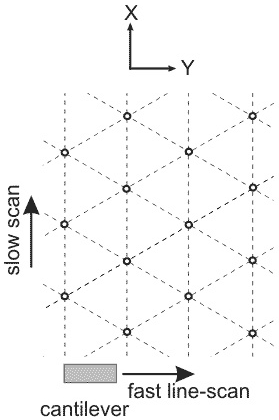
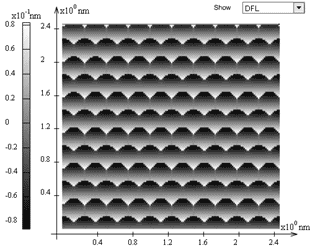
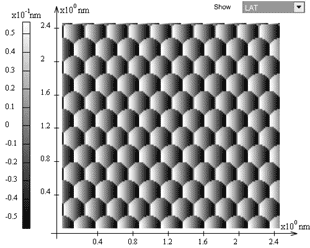
Fig. 6. (a) – cantilever and fast scan axis orientations relative to the lattice;
(b) – DFL signal distribution; (c) – LAT signal distribution.
Notice that the appearance of well or not well resolved atomic structure at scanning in different directions is not the result of the numerical model but a physical effect revealed experimentally as well [4]. In Fig. 5 and Fig. 6 are presented the calculation results obtained for two scan directions relative to the lattice.
References.
- Dedkov G.V., Uspekhi of Physical Sciences, 170 (2000) 585-618 (in Russian).
- Holscher H., Schwarz U.D., Wiesendanger R., in: Micro/Nanotribology and its Applications, ed. B. Bhushan (Kluwer, Dordrecht, 1997).
- Holscher H., Physical Review B 57 (1998) 2477-2481.
- Morita S., Fujisawa S., Sugawara Y., Surf. Sci. Rep. 23 (1996) 1-41.






