2.1.3 Deflections under the longitudinal force
In this section we determine the magnitude and direction of the deformation produced by the axial force
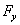 . Solution to this problem will give the middle column (2) of tensor
. Solution to this problem will give the middle column (2) of tensor
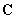 (see (2) in chapter 2.1.1).
(see (2) in chapter 2.1.1).
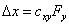
(1)
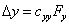
(2)
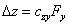
(3)
The force
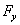 acting in the cantilever axis direction produces moment
acting in the cantilever axis direction produces moment
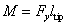 that results in deformation called here the vertical bending of y-type (Fig. 1).
that results in deformation called here the vertical bending of y-type (Fig. 1).
Fig. 1. Vertical deflection of the y-type.
In spite of the formal resemblance to vertical bending of z-type (see chapter 2.1.2), the deformation profile in this case is quite different. The equation describing the y-type bending reads (compare with (7) in chapter 2.1.2):
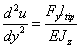
(4)
Boundary conditions remain the same:
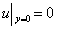 and
and
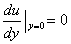 . For the solution we find:
. For the solution we find:
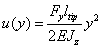
(5)
Thus, the tip vertical deflection due to this type of deformation is as follows:
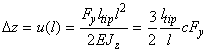
(6)
Comparing (6) and (3) and taking into account the expression for the common multiplier
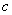 (see (12) in chapter 2.1.2), we get:
(see (12) in chapter 2.1.2), we get:
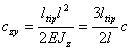
(7)
The angle of the beam end deflection
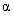 is given by the following formula:
is given by the following formula:
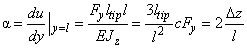
(8)
From formula (8) and diagram for the beam vertical bending of y-type (Fig. 1) it is easy to derive the tip deflection
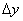 induced by the force
induced by the force
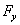 application:
application:
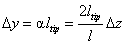
(9)
From (2), (7) and (9) it is easy to obtain:
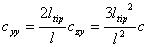
(10)
Taking into account that
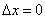 , we get:
, we get:

(11)
Finally, we calculate the components of the matrix (3) from chapter 2.1.1 second column. From expressions (6–8) it follows that
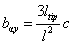
(12)
Because under the influence of the force
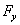 the top cantilever surface does not bend in the
the top cantilever surface does not bend in the
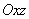 direction, then
direction, then
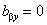
(13)
Summary.
- The y-type deflection is a result of the axial bending force action.
- To find the components of the inverse stiffness tensor corresponding to the y-type deflection, one should solve the problem of the beam static deflection which is reduced to the ordinary differential equation of the second order.
- The axial force results in the tip deflection not only in the longitudinal but also in vertical direction
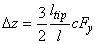 and in the deflection angle
and in the deflection angle
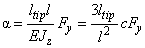 appearance.
appearance.






