2.1.2 Deflections under the vertical (normal) force component
Let us determine the magnitude and direction of the deformation arising from the vertical force
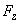 . Solution to this problem will allow to find components of the third column of tensor
. Solution to this problem will allow to find components of the third column of tensor
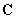 (see (2) in chapter 2.1.1).
(see (2) in chapter 2.1.1).
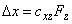
(1)
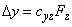
(2)
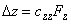
(3)
Deformation that we call here the vertical bending of z-type is shown in Fig. 1.
Fig. 1. Vertical deflection of the z-type.
Next, let's examine a section of the beam. We will cut the beam and consider the deformation of the beam element having length
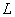 between the two cross sections (Fig. 2). Since this element is bent, the material at the outer edge is stretched in tension while at the inner edge it is compressed. Hence, there is a neutral plane of zero stress between the two surfaces. For calculations simplification we assume that the beam cross-sections remain planar and normal to their centroidal axis (pure bending of the uniform cross-section beam). This assumption is valid if
between the two cross sections (Fig. 2). Since this element is bent, the material at the outer edge is stretched in tension while at the inner edge it is compressed. Hence, there is a neutral plane of zero stress between the two surfaces. For calculations simplification we assume that the beam cross-sections remain planar and normal to their centroidal axis (pure bending of the uniform cross-section beam). This assumption is valid if
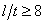 [1] which is true in our case.
[1] which is true in our case.
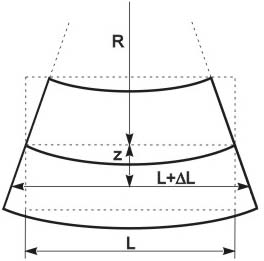
Fig. 2a. Section of the bent beam.
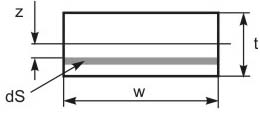
Fig. 2b. Beam cross-section.
At the pure bending the neutral plane passes through the centroid of the beam cross-sectional area [2], i.e. in our case the parallepiped long axis belongs to the neutral plane. The material longitudinal extension
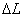 is proportional to the distance z from the neutral plane:
is proportional to the distance z from the neutral plane:
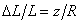 (Fig. 2). According to the Hooke's law, the force acting on a unit area in a small strip near z with square
(Fig. 2). According to the Hooke's law, the force acting on a unit area in a small strip near z with square
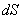 is equal to
is equal to
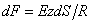 ,
where
,
where
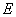 – Young's modulus,
– Young's modulus,
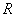 – beam curvature radius. If any cross-section is considered, the forces are acting in one direction over the neutral surface and in the other direction below it. This makes a couple of forces producing the bending moment
– beam curvature radius. If any cross-section is considered, the forces are acting in one direction over the neutral surface and in the other direction below it. This makes a couple of forces producing the bending moment
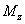 ,
which is a moment of forces with respect to the neutral axis:
,
which is a moment of forces with respect to the neutral axis:
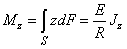
(4)
The quantity
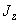 ,
is called the axial moment of inertia of the beam section about the axis that passes through its centroid. For the beam with rectangular cross-section it is given by:
,
is called the axial moment of inertia of the beam section about the axis that passes through its centroid. For the beam with rectangular cross-section it is given by:
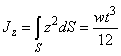
(5)
By
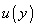 we denote the deflection of the beam point at the distance y from the fixed end in the z-direction. The curvature of the
we denote the deflection of the beam point at the distance y from the fixed end in the z-direction. The curvature of the
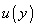 curve at small bends
(
curve at small bends
(
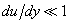 ) is given by
) is given by
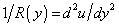 . Then, taking into account expression (5), the bending moment
. Then, taking into account expression (5), the bending moment
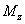 can be expressed as
can be expressed as
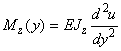
(6)
On the other hand,
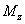 is a moment of forces with respect to point y due to the action of force
is a moment of forces with respect to point y due to the action of force
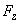 –
–
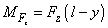 – and the beam own weight –
– and the beam own weight –
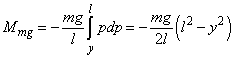 . Thus, we derive an equation:
. Thus, we derive an equation:
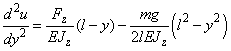
(7)
Integration of (7) having for boundary conditions
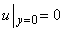 and
and
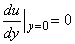 , gives:
, gives:
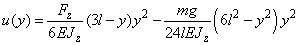
(8)
The beam end deflection
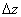 (Fig. 1) is:
(Fig. 1) is:
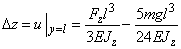
(9)
The second summand is the deflection under own weight. For a typical cantilever, it is of the fraction of the angstrom and can be neglected because in AFM experiments the first term is hundreds of time more. Relation (9) is nothing but expression (3) in which we should suppose:
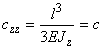
(10)
The beam deflection angle calculated without the second term in (9) is as follows:
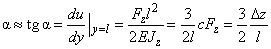
(11)
The coefficient of inverse stiffness
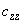 is the largest among the tensor
is the largest among the tensor
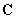 components. In (11) this parameter is specially denoted as "
components. In (11) this parameter is specially denoted as "
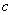 " without indexes. In particular, magnitude of
" without indexes. In particular, magnitude of
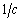 characterizes the cantilever stiffness and is one of its major parameters. Below, for the purpose of obviousness, we will take
characterizes the cantilever stiffness and is one of its major parameters. Below, for the purpose of obviousness, we will take
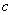 outside as a common multiplier of all the matrix
outside as a common multiplier of all the matrix
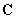 (see (2) in chapter 2.1.1) components. For a cantilever with rectangular cross-section, (11) can be rewritten as
(see (2) in chapter 2.1.1) components. For a cantilever with rectangular cross-section, (11) can be rewritten as
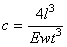
(12)
From formula (10) and diagram for the beam vertical bending of z-type (Fig. 1) it is easy to derive the tip deflection
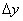 induced by the force
induced by the force
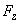 application:
application:
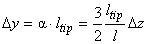
(13)
From (13) and (1), (2), (3) it is clear that
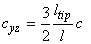
(14)
Taking into consideration that
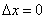 , we get
, we get
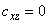
(15)
Finally, we calculate the components of the matrix (3) from chapter 2.1.1 third column. From expressions (9–12) it follows that
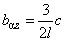
(16)
Because under the influence of the force
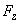 the top cantilever surface does not bend in the
the top cantilever surface does not bend in the
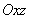 direction, then
direction, then
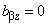
(17)
Summary.
- The z-type deflection is a result of the vertical bending force action.
- To find the components of the inverse stiffness tensor corresponding to the z-type deflection, one should solve the problem of the beam static deflection which is reduced to the ordinary differential equation of the second order.
- The vertical force results in the tip deflection in vertical and longitudinal directions and in the deflection angle
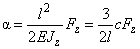 appearance.
appearance. - Besides the supporting force from the sample, the cantilever is influenced in vertical direction by its own gravity. Under this load the cantilever free end is deflected but such a deformation is small compared to minimal detected displacement.
References.
- Feynman R., Leighton R., Sands M. The Feynman Lectures on Physics, volume 7. – MIR, 1966. – 292 p. (in Russian)
- Gorshkov A.G., Troshin V.N., Shalashilin V.I. Strength of Materials. – FIZMATLIT, 2002. – 544 p. (in Russian)






