1.2.1 John G. Simmons Formula

Now, using the Sommerfeld model (see chapter 1.1.3) and WKB approximation (see chapter 1.1.2) and assuming that T = 0, potential barrier is of arbitrary shape and the mass of electrons is isotropic in space, we can derive an expression for the tunneling current flowing in a metal-insulator-metal (MIM) system.

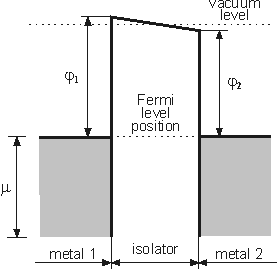
Fig. 1. Diagram of MIM system in equilibrium.
j₁ and j₂ – work function of the left and right metals, respectively.

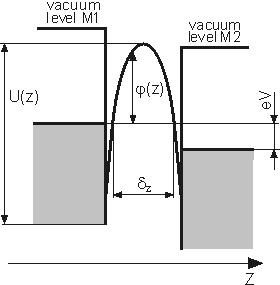
Fig. 2. Model of MIM system with an arbitrary shape potential
barrier. Positive potential is applied to the right metal.

Consider two metal electrodes with an insulator of thickness L between them. If electrodes are under the same potential, the system is in thermodynamic equilibrium (see chapter 1.1.3) and Fermi levels of electrodes coincide (Fig. 1). However, if electrodes are under different potentials, current flow between them is available. Fig. 2 shows the energy diagram of electrodes with applied bias energy eV. Potential barrier width for electrons occupying the Fermi level is denoted as d_z = z₂ – z₁. Consider that all the current flowing in the system is due to the tunneling effect.

Probability D(E_z) of the electron transmission through the po-tential barrier of height U(z) is given by expression (4) in chapter 1.1.2. For the number of electrons N₁ tunneling through the barrier from electrode 1 into electrode 2, we can write [1, 2]

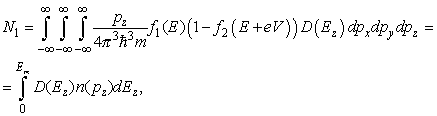
(1)

where

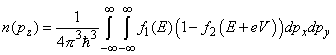
(2)

and E_m – maximum energy of tunneling electrons.

Integration of expression (2) can be performed in polar coordinates. Because in the model under consideration 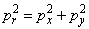, 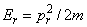and total energy is 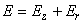, changing variables 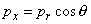, , 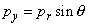we get

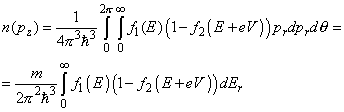
(3)

Substituting (3) in (1), we obtain

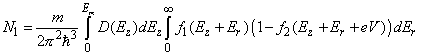
(4)

The number of electrons N₂ tunneling back from electrode 2 into electrode 1 is calculated in the same way. According to (4) from chapter 1.1.2, the potential barrier transparency in the given case will be such as if positive voltage V is applied to electrode 1 relative to electrode 2. In this case

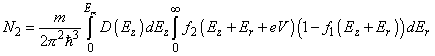
(5)

Net electrons flow N through the barrier is obviously N = N₁ – N₂. Let us denote

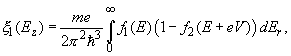
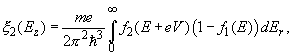
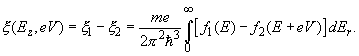
(6)

Then, the tunneling current density J is

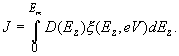
(7)

According Fig. 2, U(z) can be written in the form 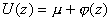. Then, integrating (4) from chapter 1.1.2 and using expression (A5) from Appendix, we get

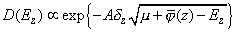
(8)

where 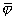– average barrier height relative to Fermi level of the negative electrode; 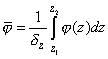; 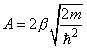, b – dimensionless factor defined in the Appendix (A6).

At T = 0 K

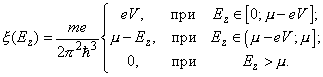
(9)

Introducing (8) and (9) into (7), we obtain

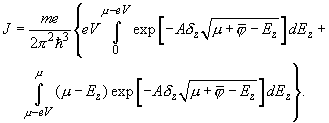
(10)

Integrating (10), we get

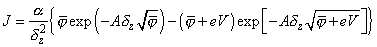
(11)

where .

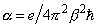Thus, expression (11) approximates the tunneling current in the MIM system for arbitrary barrier shape.

Summary.

The general expression (7) to calculate the tunneling current in the MIM system was derived in this chapter.
The analytic approximate solution (11) of tunneling current in the MIM system was calculated.

References.

Burshtein E., Lundquist S. Tunneling phenomena in solid bodies. Mir, 1973 (in Russian)
John G. Simmons. J. Appl. Phys. - 1963. - V. 34 1793.
John G. Simmons. J. Appl. Phys. - 1963. - V. 34 238.