1.1.2 Tunneling Effect in Quasiclassical Approximation
The quasiclassical qualitative condition imply that de Broglie wavelength of the particle
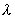 is less than characteristic length
is less than characteristic length
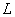 determining the conditions of the problem. This condition means that the particle wavelength should not change considerably within the length of the wavelength order
determining the conditions of the problem. This condition means that the particle wavelength should not change considerably within the length of the wavelength order
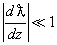 ,
,
(1)
where
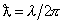 ,
,
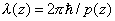 – de Broglie wavelength of the particle expressed by way of the particle classical momentum p(z) [1].
– de Broglie wavelength of the particle expressed by way of the particle classical momentum p(z) [1].
Condition (1) can be expressed in another form taking into account that
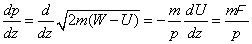 ,
,
(2)
where
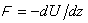 means classical force acting upon the particle in the external field.
means classical force acting upon the particle in the external field.
Introducing this force, we get
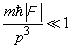
(3)
From (3) it is clear that the quasiclassical approximation is not valid at too small momentum of the particle. In particular, it is deliberately invalid near positions in which the particle, according to classical mechanics, should stop, then start moving in the opposite direction. These points are the so called "turning points". Their coordinates
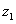 and
and
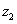 are determined from the condition
are determined from the condition
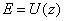 .
.
It should be emphasized that condition (3) itself can be insufficient for the permissibility of the quasiclassical approach. One more condition should be met: the barrier height should not change much over the length
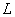 .
.
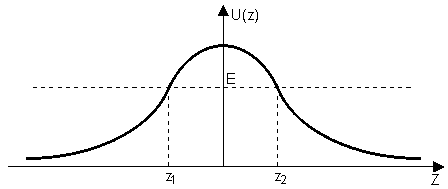
Let us consider the particles move in the field shown in Fig. 1 which is characterized by the presence of the potential barrier with potential energy
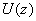 exceeding particle total energy
exceeding particle total energy
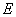 and meeting all the quasiclassics conditions. In this case points
and meeting all the quasiclassics conditions. In this case points
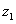 and
and
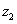 are the turning points.
are the turning points.
 ,
,
Fig. 1. Potential barrier of arbitrary shape.
The approximation technique of the Schrodinger equation solution when quasiclassical conditions are met was first used by Wentzel, Kramers and Brillouin. This technique is known as WKB approximation or quasiclassical quantization method. In this textbook we do not present the Schrodinger equations solution for the given case. However, it can be found in [1, 2] and the barrier transparency in this case is
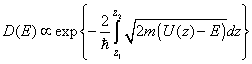 ,
,
(4)
Comparing expressions (3) in chapter 1.1.1 for transmission coefficients of rectangular barrier (precise solution of Shrodinger equation) and (4) for quasiclassical approximation, we can notice that there is no qualitative difference between them. In both cases the transparency decreases exponentially with the barrier width.
Summary.
- If the problem parameters satisfy quasiclassical conditions, then transmission coefficient can be calculated in a general form using (4).
- In case of the square barrier there is no qualitative difference between transmission coefficients calculated using quantum mechanics and quasiclassical approximation. In both cases the transparency decreases exponentially with the barrier width.
References.
- Landau L.D., Lifshitz E. M. Quantum mechanics. Nauka, 1989 (In Russian)
- Mott N., Sneddon I. Wave mechanics and its application. Nauka, 1966 (In Russian)






