1.1.1 Tunneling Effect
The idea of particles tunneling appeared almost simultaneously with quantum mechanics. In classical mechanics, to describe a system of material points at a certain moment of time, it is enough to set every point coordinates and momentum components. In quantum mechanics it is in principle impossible to determine simultaneously coordinates and momentum components of even single point according to the He-isenberg uncertainty principle. To describe the system completely, an associated complex function is introduced in quantum mechanics (the wavefunction). The wavefunction
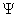 , which is a function of time and all system particles position, is a solution of the wave Schrodinger equation. In order to use the system wavefunction, one should determine
, which is a function of time and all system particles position, is a solution of the wave Schrodinger equation. In order to use the system wavefunction, one should determine
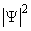 rather than
rather than
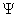 . Then, the probability for finding particles in an elementary volume dxdydz is given by
. Then, the probability for finding particles in an elementary volume dxdydz is given by
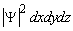 .
.
If particles impinge on a potential barrier of a limited width, the quantum mechanics predicts the effect of particles penetration through the potential barrier even if particle total energy is less than the barrier height which is unknown in classical physics.
Lets calculate the transparency of the rectangular barrier [1, 2]. Suppose that electrons of potential energy
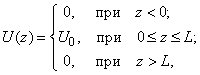
(1)
impinge on the rectangular potential barrier and the total energy E is less than U0 (Fig. 1).
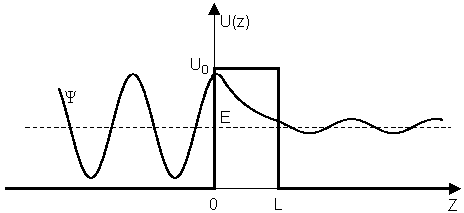
Fig. 1. Rectangular potential barrier and particle wave function
 .
.
The stationary Schrodinger equations can be written as follows
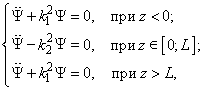
(2)
where
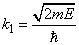 ,
,
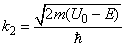 – wave vectors,
– wave vectors,
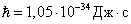 – Planck's constant. The solution to the wave equation at
– Planck's constant. The solution to the wave equation at
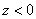 can be expressed as a sum of incident and reflected waves
can be expressed as a sum of incident and reflected waves
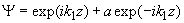 , while solution at
, while solution at
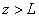 – as a transmitted wave
– as a transmitted wave
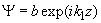 . A general solution inside the potential barrier
. A general solution inside the potential barrier
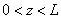 is written as
is written as
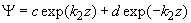 . Constants a, b, c, d are determined from the wavefunction
. Constants a, b, c, d are determined from the wavefunction
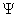 and
and
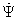 continuity condition at
continuity condition at
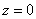 and
and
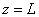 .
.
The barrier transmission coefficient can be naturally considered as a ratio of the transmitted electrons probability flux density to that one of the incident electrons. In the case under consideration this ratio is just equal to the squared wavefunction module at
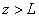 because the incident wave amplitude is assumed to be 1 and wave vectors of both incident and transmitted waves coincide.
because the incident wave amplitude is assumed to be 1 and wave vectors of both incident and transmitted waves coincide.
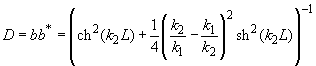
(3)
If
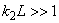 , then both
, then both
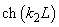 and
and
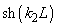 can be approximated to
can be approximated to
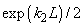 and (3) will be written as
and (3) will be written as
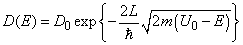
(4)
where
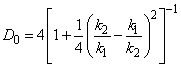 .
.
Thus, analytical calculation of the rectangular barrier transmission coefficient is rather a simple task. However, in many quantum mechanical problems it is necessary to find the transmission coefficient of the more complicated shape barrier. In this case, there is no common analytical solution for the D coefficient. Nevertheless, if the problem parameters satisfy the quasiclassical condition, the transmission coefficient can be calculated in a general form. (see chapter 1.1.2).
Summary.
- In quantum mechanics tunneling effect is particles penetration through the potential barrier even if particle total energy is less than the barrier height.
- To calculate the transparency of the potential barrier, one should solve Shrodinger equation at continuity condition of wavefunction and its first derivative.
- The transparency coefficient of the rectangular barrier decreases exponentially with the barrier width, when wave vectors of both incident and transmitted waves coincide.
References.
- Sivuhin D.V. A General course of physics. Nauka, volume 5, chapter 1, 1988 (In Russian)
- Goldin L.L., Novikova H.I. The introduction in quantum physics. Nauka, 1988 (In Russian).






