1.1.3 Metal Energy-Band Structure
To derive the formula of tunneling current in the metal-insulator-metal (MIM) system (John G. Simmons formula, see chapter 1.2.1), we must make some assumptions and remind of metal electronic theory fundamentals.
- Firstly, let us consider that the solid (metal) is a three-dimensional potential well with a plane bottom (the so called Sommerfeld model) and electrons do not interact with each other. The energy of the electron resting at the bottom of such potential well is less than vacuum level – the energy of electron resting infinitely far from the solid surface. The well depth U is determined by the averaged field of all positive ions of the lattice and of all electrons.
- Secondly, because all electrons are considered to be noninteracting, the solution to the Schrodinger equation for the system of electrons is turned to the solution to the Schrodinger equation for single electron moving in the averaged field which allows to use formulas (3) in chapter 1.1.1 or (4) in chapter 1.1.2.
- Thirdly, in the potential box with the plain bottom, the dependence of energy allowed values on wave vector allowed values looks like points on the parabolic dependence of the energy on the wave vector components
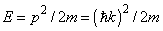 for the free electron in void. If electrons mass m is isotropic in space, then the following expression is valid
for the free electron in void. If electrons mass m is isotropic in space, then the following expression is valid
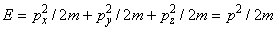 , where
, where
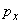 ,
,
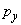 ,
,
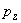 – axial electron momentum components.
– axial electron momentum components.
From the statistical physics [1] it is known that in a system in thermodynamic equilibrium all quantum states with the same energy level E are occupied with electrons equally. The mean number of electrons in one quantum state with energy E at temperature T is given by the Fermi-Dirac distribution:
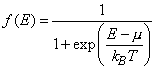
(1)
where
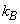 = (11600)–1 eV/К – Boltzmann's constant,
= (11600)–1 eV/К – Boltzmann's constant,
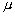 – parameter having the dimension of energy and called chemical potential.
– parameter having the dimension of energy and called chemical potential.
The chemical
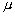 potential is defined by the normalization condition
potential is defined by the normalization condition
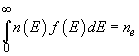
(2)
where ne – number of conduction band electrons per volume unit (concentration),
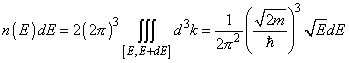 – number of elecron states per volume unit in the energy range from E to E + dE. n(E) function is called the energetic density of states.
– number of elecron states per volume unit in the energy range from E to E + dE. n(E) function is called the energetic density of states.
In a metal at the temperature close to absolute zero, electrons occupy all quantum states with energies up to the level
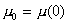 called the Fermi level. All quantum states above the Fermi level are not occupied with electrons. In a metal, the chemical potential slightly depends on temperature, therefore it can be approximated by
called the Fermi level. All quantum states above the Fermi level are not occupied with electrons. In a metal, the chemical potential slightly depends on temperature, therefore it can be approximated by
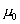 at T = 0:
at T = 0:
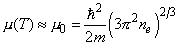
(3)
where m – electron mass. If ne is expressed in C.G.S. units, then
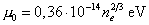 .
.
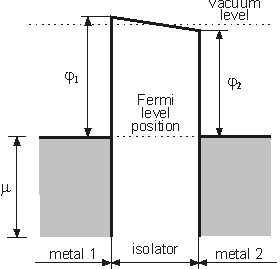
Fig. 1. Diagram of MIM system in equilibrium.
j1 and j2 – work function of the left and right metals, respectively.
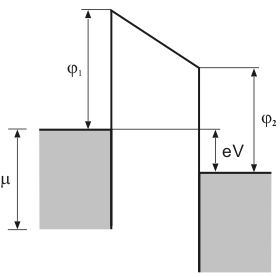
Fig. 2. Model of MIM system then positive potential is applied to the right metal.
If a system is in thermal equilibrium and consists of some sub-systems, the Fermi levels of subsystems should be the same (Fig. 1). If voltage V is applied between two subsystems (solids), the Fermi level of the solid connected to the positive pole decreases, while for the other solid it increases. The difference in Fermi levels between solids is eV (Fig. 2).
Summary.
To derive the formula of tunneling current in the MIM system (chapter 1.2.1) we assume that:
- Sommerfeld model is correct for all solid bodies.
- Each electron from the solid move in averaged field of all positive ions of the lattice and of all electrons.
- Isotropic square-law of dispersion as for free electron in void is correct (1).
- In a metal at
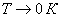 , electrons occupy all quantum states with energies up to the Fermi level
, electrons occupy all quantum states with energies up to the Fermi level
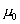 (3). All quantum states above the Fermi level are not occupied with electrons.
(3). All quantum states above the Fermi level are not occupied with electrons.
References.
- Landau L.D., Lifshitz E. M. Statistical physics. Nauka, 1976 (in Russian)
- Kittel Ch. Introduction in solid-state physics. Nauka, 1978 (in Russian)






