1.2.1 Appendix
Let us integrate an arbitrary function
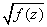from
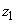to
.
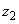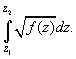
(A1)
Defining
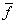as
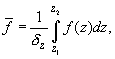
(A2)
where
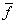– average value of a function
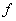on the interval from
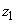to
,
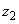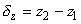. Then equation (A1) can be rewritten as
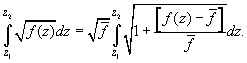
(A3)
Considering a Taylor series expansion of the integrand (A3) in and neglecting
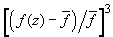and higher order members, we get
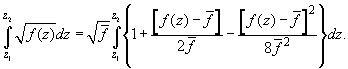
(A4)
The second term in (A4) vanishes upon integration, therefore (A4) can be expressed as
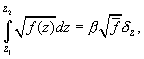
(A5)
where the correction factor is
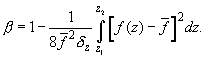
(A6)