2.4.1 Qualitative consideration

Consider a cantilever oscillations when in addition to driving force ((1) in chapter 2.3.3), an external force 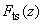acts on it. The equation of motion in this case is written as

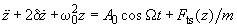
(1)

In a general case the steady-state solution of equation (1) is the sum of harmonics with frequencies divisible by a driving force frequency :

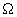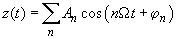
(2)

In chapter 2.3.4 we considered the particular case of equation (1) solution - small oscillations when the following condition is met

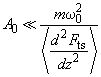
(3)

where 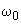– cantilever natural resonant frequency, 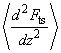– mean of the second derivative of the tip-sample interaction force (averaged with respect to oscillations amplitude.

In practice, condition (3) is seldom met. However, utilizing numerical methods, one can show that even under weak condition (4), the character of steady-state oscillations will only slightly differ from harmonic (a major contribution is made only by the first harmonic)

condition

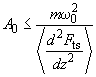
(4)

solution

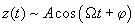
(5)

In contrast to the case of small oscillations where the steady-state condition is entirely determined by system parameters, the motion in the considered case depends on the initial state. That is, depending on the initial position of the cantilever relative to the equilibrium position, the character of the steady-state oscillations will vary (Fig. 1).

Fig. 1. Feasibility of several quasisteady-state solutions obtaining.

This feature results, in its turn, in the resonance curves (AFC and PFC) distortion. Fig. 2 shows dependences of amplitude-frequency and phase-frequency characteristics of the system on the driving force amplitude.

Fig. 2. Resonance curves in case of nonlinear oscillations.

The cantilever approach-retraction curves (see chapter 2.3.5) are distorted too, which can result in impossibility to render the character of the derivative and parameters of the tip-sample interaction force. In Fig. 3 are shown the cantilever approach curves for different amplitudes of the driving force.

Fig. 3. Tip-sample approach curves for different amplitudes of the driving force.

Summary.

Influence of an external force 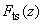in a general case is the deviation from the oscillatory motion. If, however, the condition for the driving force amplitude is weak (4), the oscillation is almost harmonic (a major contribution is made only by the first harmonic).
In contrast to the case of small oscillations where the steady-state condition is entirely determined by system parameters, the motion in the considered case depends on the initial state.