2.1.5 Cantilever inverse stiffness tensor
Let us write the obtained components of inverse stiffness tensor
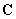 (see (2) in chapter 2.1.1) into the representative matrix for mathematical convenience:
(see (2) in chapter 2.1.1) into the representative matrix for mathematical convenience:
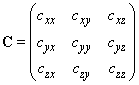
(1)
The
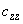 coefficient of inverse stiffness is the largest of other tensor
coefficient of inverse stiffness is the largest of other tensor
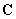 components. In formula (12) of chapter 2.1.2 this parameter is specially denoted as
components. In formula (12) of chapter 2.1.2 this parameter is specially denoted as
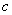 without indexes. It is namely the quantity
without indexes. It is namely the quantity
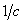 that characterizes a cantilever stiffness which is one of its major parameters. Below, for the sake of clearness, we will take
that characterizes a cantilever stiffness which is one of its major parameters. Below, for the sake of clearness, we will take
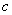 outside as a common multiplier of all the matrix elements [1]:
outside as a common multiplier of all the matrix elements [1]:
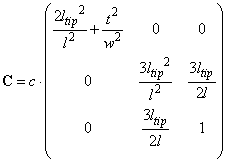
(2)
Tensor
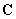 is symmetric. That is true. The left side of expression (1) in chapter 2.1.1 –
is symmetric. That is true. The left side of expression (1) in chapter 2.1.1 –
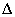 is a polar vector, therefore, the right side must have the same transformational properties. The force
is a polar vector, therefore, the right side must have the same transformational properties. The force
 is a polar vector; therefore, the tensor must be symmetric in order to properly transform the expression (2) in chapter 2.1.1 at coordinates reflections.
is a polar vector; therefore, the tensor must be symmetric in order to properly transform the expression (2) in chapter 2.1.1 at coordinates reflections.
The presence of non-diagonal elements leads to the difference in directions of the applied force and of the tip deflection vector and is an evidence of limited applicability of the elastic cantilever simplified model based on three perpendicular springs. To apply this model, one should determine not only stiffness but true directions of three springs that do not coincide with coordinate axes. This problem is reduced to the tensor (2) diagonalization in order to obtain its eigenvalues as well as to determine the directions of transformed co-ordinates along which the model springs should be oriented.
It is seen that the cantilever elastic properties are completely defined by five parameters. We can find all tensorial components knowing geometrical characteristics of the cantilever and its stiffness constant.
To facilitate computation at experiments, the obtained components are introduced into the matrix in formula (3) of chapter 2.1.1:
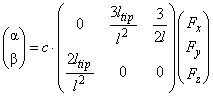
(3)
Summary.
- The tensor component
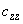 corresponding to the vertical displacement at z-type deflection is the largest. Its inverse value is the beam stiffness constant that characterizes a cantilever.
corresponding to the vertical displacement at z-type deflection is the largest. Its inverse value is the beam stiffness constant that characterizes a cantilever. - Tensorial nature of a cantilever elastic properties leads to the limited applicability of simplified models based on springs.
- To properly model a cantilever elastic properties by three springs, one should determine their parameters correctly by diagonalization of the inverse stiffness tensor.
References.
- Handbook of Micro/Nanotribology / Ed. by Bhushan Bharat. - 2d ed. - Boca Raton etc.: CRC press, 1999. – 859 c.






