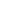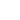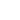2.7.6 Interaction between soft magnetic probe and magnet sample
In chapter 2.7.3 we described the general model of a hard magnetic probe interaction with a magnetic field of a sample and neglected the fact that a tip and a sample can mutually affect their magnetic characteristics. This influence should, in fact, be taken into account when constructing theoretical models of a hard magnetic tip interaction with the sample magnetic field. An assumption that the sample magnetization is not affected by the tip magnetic field is a good approximation for hard magnetic samples and is not valid for the soft ones, for example, for
 (permalloy) [1-3].
(permalloy) [1-3].
In [4] it is shown that the tip magnetic field affects the magnetic properties of the sample and vice-versa in case when magnetic field of one exceeds the magnetic anisotropy field of the other:
 or
or

(1)
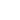
where
 and
and
 – magnetic fields of tip and sample and, respectively,
– magnetic fields of tip and sample and, respectively,
 ,
,
 – magnetic anisotropy fields. Near the tip and sample surface the magnetic field can be taken equal to
– magnetic anisotropy fields. Near the tip and sample surface the magnetic field can be taken equal to
 , where
, where
 – a material magnetization, and can exceed much the magnetic anisotropy field of a soft magnetic material like iron or permalloy. To avoid this effect it is necessary to increase the tip-sample separation [5] that results in sufficient lateral resolution deterioration.
– a material magnetization, and can exceed much the magnetic anisotropy field of a soft magnetic material like iron or permalloy. To avoid this effect it is necessary to increase the tip-sample separation [5] that results in sufficient lateral resolution deterioration.
In [2,3] the theories were developed that take into account the magnetization vector rotation under the external magnetic field. These theories predict the appearance of an additional attraction force between a tip and a sample because magnetic moments in a sample tend to align with the tip magnetic field and vice-versa. This effect was observed in permalloy [5].
Perhaps, the most successful way of the tip-sample interaction description is the determination of a system minimum energy. The method is a sample decomposition into infinitesimal cells and a subsequent calculation of the minimum energy of magnetic states taking into consideration the exchange interaction, anisotropy energy and magnetostatics. In [6] this method was used for the calculation of the permalloy domain walls distribution in the presence of the iron tip. In [7] the energies of the tip magnetic states equilibrium and the resultant force acting on it in the magnetic field was calculated by integration of the Landau-Lifshits-Hilbert equation.
Summary.
- In case when magnetic field of a sample exceeds the magnetic anisotropy field of a tip and vice-versa, they can mutually affect the magnetic characteristics of each other.
- Presented is a brief review of quantification methods of a soft magnetic tip interaction with a sample magnetic field and, accordingly, a soft magnetic sample interaction with a tip magnetic field.
References.
- T. Goodenhenrich, U. Hartmann, M. Anders, C. Heiden: J. Microscopy 152, 527 (1988).
- J.J. Saenz, N. Garcia, J.C. Slonczewski; Appl. Phys. Lett. 53, 1449 (1988).
- D.W. Abraham, F.A. McDonald: Appl. Phys. Lett. 56, 1181 (1990).
- U. Hartamnn: J. Appl. Phys. 64, 1561 (1988).
- H.J. Mamin, D. Rugar, J.E. Stern, R.E. Fontana, Jr., P. Kasiraj: Appl. Phys. Lett. 55 318 (1989).
- M.R. Scheinfein et al. J. Appl. Phys. 67, 5932 (1990).
- M. Mansuripur: IEEE Trans. Magn. 25, 3467 (1989).