2.5.1 The effect of elastic deformations

The AFM technique accuracy is limited by elastic deformations which modify a sample topography. One of the effects of this kind, the indentation of large organic molecules surface (Appendices of the Hertz problem), results in the measured height decrease by several tens of percent. The same phenomenon can be expected when scanning across tilted, convex or concave surface areas (Fig. 1).

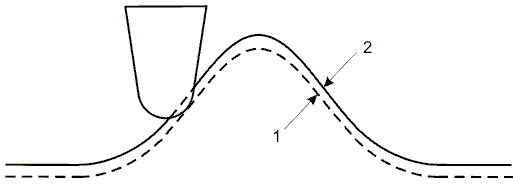
Fig. 1. Scan line profile (1) vs. original surface topography (2). Due to elastic deformations the surface convex feature shape
is lower and narrower than the original.

The Hertz problem solution allows to estimate the best reliable resolution during measurements. Let us use formula (3) in chapter 2.2.2.2 which we rewrite as:

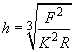
(1)

where 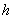– depth of tip and sample mutual penetration, 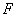– applied force, 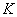– tip-sample effective Young's modulus (see formula (1) in chapter 2.2.2.2), 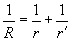, where 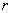, 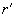– tip and sample curvature radii, respectively.

Formulation of the Hertz problem implies that penetration depth 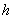is much less than curvature radius 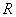; this limitation, however, can be neglected in estimations. Let us calculate the minimum characteristic size of the surface feature which is of the order of the deformation under the tip action, i.e. we assume that in (1) 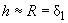. The scale 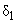can be considered as the resolution limit due to elastic deformations:

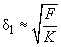
(2)

This expression approximates both vertical and lateral resolution limit for the small features.

Notice that not only small but larger surface features ( ) can be imaged with shape distortion. If vertical elastic indentation (1) for the large features is practically the same as for the small ones ( ) and thus can be neglected, the lateral shift of the inclined areas image must be taken into consideration because the shift sign depends on the inclination (Fig. 1).

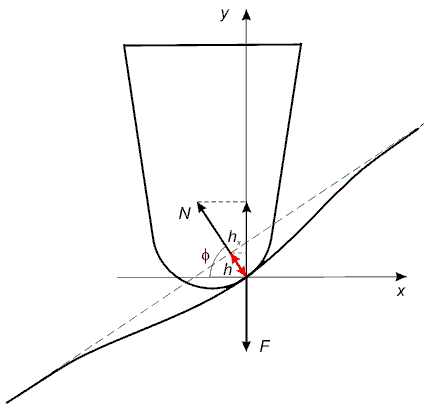
Fig. 2. Indentation during scanning of inclined area.

Examine now Fig. 2. The vertical pressing force causes the sample normal reaction force which at the inclined area is given by:

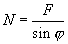
(3)

The arising deformation 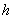is directed normal to the surface. Its horizontal component is:

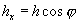
(4)

This component gives rise to the image distortions when scanning across inclined surface areas and can be taken as the lateral resolution limit due to elastic deformations. Substitute 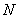instead of 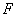in formula (1) in accordance with (2), use (4) and assume for large surface features 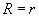. Then:

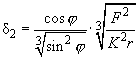
(5)

The obtained expression diverges at 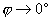; however, one should remember that the slope of the contact area can not exceed half the tip cone angle. That's why for the limit upper estimate (5) one should take namely this value as 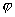. For the typical tip cone angle 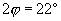, the first multiplier in expression (5) second member is approximately equal to 3.

As a lateral resolution, one should choose the largest of quantities 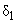(2) and 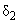(5) depending on experimental parameters 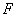, , 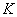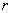values. If

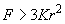
(6)

formula (5) should be used, otherwise – formula (2).

Let us calculate the resolution limit for the silicon cantilever with tip curvature radius 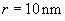and cone angle 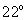probing materials with various elastic moduli. In table 1, the resolution values that satisfy condition (6) are marked gray, the other values satisfy condition (2).


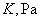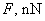	0.1	1	10	100
10⁸	1.4	6.4	30	140
10⁹	0.32	1.4	6.4	30
10¹⁰	0.10	0.32	1.4	6.4
10¹¹	0.03	0.10	0.32	1.4
10¹²	0.01	0.03	0.10	0.32

Table 1. Lateral resolution limit, nm

Summary.

Elastic deformation of the surface features by the tip leads to the AFM image distortion which results in poor resolution.
Small features with sizes of the order of the deformation value can not be resolved. For the objects with curvature radius less than the tip radius, the resolution is approximated by .
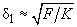On the other hand, the image resolution is limited by the deflection at the sample inclined areas and is equal to .
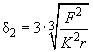