2.2.2.5 Appendices
Appendix 1.
An interesting fact is that if one sets equal scan parameters and uses the same probe when studying hard and soft samples, the first one can be damaged while the second can stay undamaged.
Consider two cases of scanning flat samples from mica and pyrolytic graphite. A silicon probe with known characteristics is used. Let us calculate the contact pressure developed under the same load force
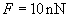 and compare it with the ultimate strength of respective materials.
and compare it with the ultimate strength of respective materials.
The following values are used:
-
Tip curvature radius:
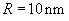
-
Load force:
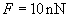
-
Moduli of elasticity:
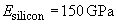 [1, 2],
[1, 2],
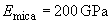 [2],
[2],
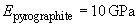 [2]
[2]
-
Ultimate strength:
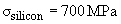 [2],
[2],
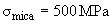 [2],
[2],
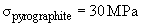 [2]
[2]
To find the "effective elasticity"
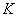 we use formula (1) in chapter 2.2.2.2 where for the sake of simplicity Poisson's ratios are ignored.
we use formula (1) in chapter 2.2.2.2 where for the sake of simplicity Poisson's ratios are ignored.
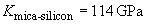
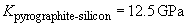
Substitution of values into formula (4) in chapter 2.2.2.2 yields:
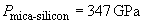
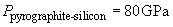
It is clear that the softer sample can not be damaged. This, as pointed out before, arises from the fact that for hard materials the contact area is very small so the pressure is much larger as compared to softer materials.
Appendix 2.
The possibility of the sample or the tip destruction depends on the scan speed in the contact mode. If during static measurements or slow scanning the load can exceed the critical value, the destruction can occur not at high cantilever speed.
The reason is as follows: though at high probe speed the deformations at every point are "overcritical", their duration is small so the sample has no time to be destroyed.
Because the scan speed depends on the scan area, the effect can suddenly manifest itself while changing the image size when its decreasing results in the sample damage.
Let the pyrolitic graphite sample be imaged by the silicon cantilever. The goal is to choose such scanning parameters that materials in contact are not damaged.
The following values are used:
-
Tip curvature radius:
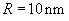
-
Load force:
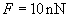
-
Moduli of elasticity:
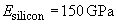 [1, 2],
[1, 2],
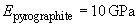 [2]
[2]
-
Ultimate strength:
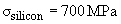 [2],
[2],
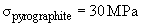 [2]
[2]
-
Elastic relaxation time:
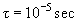
To find the "effective elasticity"
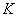 we use formula (1) in chapter 2.2.2.2 where for the sake of simplicity Poisson's ratios are ignored.
we use formula (1) in chapter 2.2.2.2 where for the sake of simplicity Poisson's ratios are ignored.
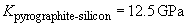
The radius of the contact area arising from the force
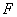 action can be expressed from formula (3) in chapter 2.2.2.2:
action can be expressed from formula (3) in chapter 2.2.2.2:
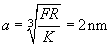
Let cantilever be moved with horizontal speed
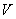 . The time of the tip action upon the given point (i.e. the time of tip travel across the contact area diameter) should be less than the relaxation time:
. The time of the tip action upon the given point (i.e. the time of tip travel across the contact area diameter) should be less than the relaxation time:
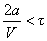
The speed, in turn, is the line length multiplied by the line scan frequency
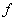 –
–
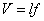 . Therefore, materials will not be destroyed if:
. Therefore, materials will not be destroyed if:
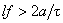 i.e.
i.e.
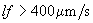
For example, if line scan frequency is
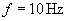 , the minimum permissible scan area dimension is
, the minimum permissible scan area dimension is
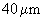 .
.
Appendix 3.
Due to the elastic penetration of the tip into the sample the scan line profile differs from the real geometry.
Let us determine the silicon cantilever penetration into the large organic molecule.
The following values are used:
-
Tip curvature radius:
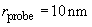
-
Molecule dimension:
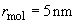
-
Load force:
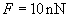
-
Moduli of elasticity:
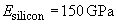 [1, 2],
[1, 2],
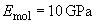 [2]
[2]
To find the "effective elasticity"
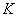 we use formula (1) in chapter 2.2.2.2 where for the sake of simplicity Poisson's ratios are ignored.
we use formula (1) in chapter 2.2.2.2 where for the sake of simplicity Poisson's ratios are ignored.
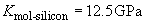
Using formula (3) in b>chapter 2.2.2.2 the penetration depth
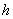 can be expressed as:
can be expressed as:
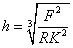
where
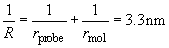
Calculation gives
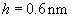 which is more than 10% of the molecule dimension.
which is more than 10% of the molecule dimension.
Appendix 4.
While studying microobjects placed onto the substrate, one should notice that the tip penetration results in a height lowering of small particles. It was experimentally proved that this lowering can reach tens percent of the undeformed molecule dimension.
In order to calculate the profile change it is necessary to know not only the tip penetration into the microparticle
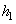 (see Appendix 3) but "particle-substrate" penetration depth
(see Appendix 3) but "particle-substrate" penetration depth
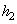 and "tip-substrate" penetration
and "tip-substrate" penetration
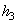 . As seen in Fig. 1, the height lowering is:
. As seen in Fig. 1, the height lowering is:
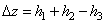
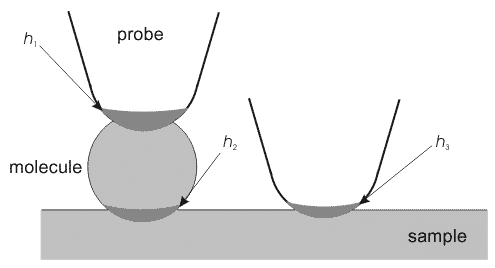
Fig. 1. On the calculation of height lowering when scanning large molecules.
Let the large organic molecule placed onto the flat graphite substrate be scanned by the silicon cantilever. The height lowering will be calculated using the following values:
-
Tip curvature radius:
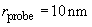
-
Molecule dimension:
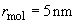
-
Load force:
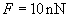
-
Moduli of elasticity:
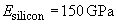 [1, 2],
[1, 2],
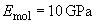 [2],
[2],
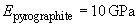 [2]
[2]
Calculation of the penetration for every pair of materials is performed like in Appendix 3:
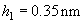
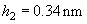
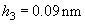
Total:
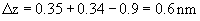 .
.
References.
- Physical magnitudes. Reference book/ Ed. Grigor'ev I.S., Meilikhova I.Z.. – Moscow: Energoatomizdat Publ., 1991. – 1231 pp.
- Gallyamov M.O., Yaminsky I.V. Scanning probe microscopy: basic principles, distortions analysis (218 kB).






