2.4.3 Method of resonance characteristics calculation. Approach-retraction curves
In chapter 2.4.2 we presented the approximate method of solution to the tip equation of motion in an arbitrary potential field. It was shown that the resonance characteristics of the probe-sample system are expressed by:
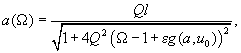
(1)
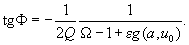
(2)
Equations (1,2) relate amplitude, phase and driving force frequency implicitly. In order to facilitate the calculation of resonance characteristics consider the following method. Let us obtain from (1) the inverse dependence of driving force frequency on oscillations amplitude. It can be easily shown that:
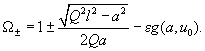
(3)
Expression (3) describes two branches of the system AFC where "+" sign corresponds to the branch
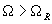 while "-" – to
while "-" – to
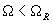 branch. A new designation
branch. A new designation
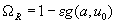 is introduced here. Now, although there are two branches instead of one, the dependence of frequency on amplitude is explicit. Next, using expression (2) we can obtain complete resonance characteristics of the system:
is introduced here. Now, although there are two branches instead of one, the dependence of frequency on amplitude is explicit. Next, using expression (2) we can obtain complete resonance characteristics of the system:
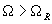
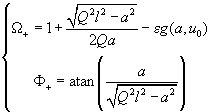
(4)
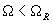
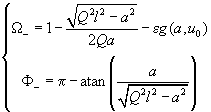
(5)
where oscillation amplitude is a parameter changing within the range
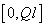 .
.
Both branches join at a point of maximum oscillation amplitude (resonance)
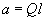 . To this magnitude of amplitude corresponds the driving force frequency
. To this magnitude of amplitude corresponds the driving force frequency
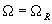 . Thus,
. Thus,
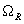 is the system resonance frequency at probe-sample distance
is the system resonance frequency at probe-sample distance
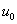 .
.
We can now determine how the system resonance frequency changes with the probe-sample distance. Recalling the introduced above definition of auxiliary function
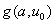 (see (9) in chapter 2.4.2), the relative shift of the resonance frequency can be written as
(see (9) in chapter 2.4.2), the relative shift of the resonance frequency can be written as
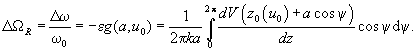
(6)
Thus, the expression for the change in the resonance frequency of the cantilever when it is retracted from the sample, contains information about the interaction potential character.
If the oscillation amplitude is small, i.e.
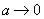 , expression (6) can be rewritten in the form:
, expression (6) can be rewritten in the form:
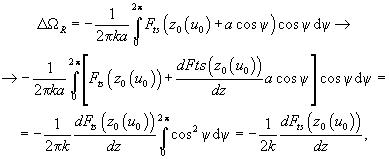
(7)
where
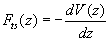 stands for the tip-sample interaction force. Recalling the theory of a cantilever small oscillations in the field of force
stands for the tip-sample interaction force. Recalling the theory of a cantilever small oscillations in the field of force
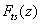 , we can see that the expression for the resonance frequency shift is exactly the same as expression (7).
, we can see that the expression for the resonance frequency shift is exactly the same as expression (7).
To obtain the amplitude-distance dependence during the tip retraction, assume that the cantilever is excited at the frequency equal to its natural resonance frequency and interaction is absent, i.e.
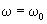 and, accordingly,
and, accordingly,
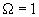 . From the character of the system AFC it easily follows that
. From the character of the system AFC it easily follows that
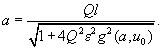
(8)
Expression (8) can be written in the form
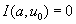 which sets the character of the oscillation amplitude dependence on the probe-sample distance. Solution of (8) can in some cases be ambiguous (depending on interaction potential and probe-sample separation) that corresponds to the simultaneous existence of several oscillation modes with different amplitudes and, correspondingly, phases, because from (2) the phase of oscillation is the unique function of amplitude.
which sets the character of the oscillation amplitude dependence on the probe-sample distance. Solution of (8) can in some cases be ambiguous (depending on interaction potential and probe-sample separation) that corresponds to the simultaneous existence of several oscillation modes with different amplitudes and, correspondingly, phases, because from (2) the phase of oscillation is the unique function of amplitude.
Consider the case of small oscillations. As it was shown for the case of the resonance frequency shift, in the given case the following is true:
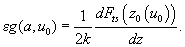
(9)
Substituting (9) into (8), we get
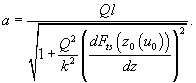
(10)
If a vertical gradient of the tip-sample interaction force is small, the relative amplitude variation can be expressed as:
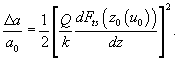
(11)
Comparing the obtained expression with that derived using the theory of small amplitude oscillations, it is easily seen that both theories give exactly the same results.
Consider now the oscillation phase shift occurring during the tip retraction. Similarly to the amplitude case we assume
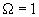 . Taking into account (2), we obtain:
. Taking into account (2), we obtain:
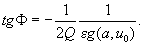
(12)
Using the condition for small oscillations (9), expression (12) is transformed into:
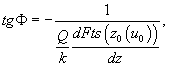
(13)
which again corresponds exactly to that derived in the theory of small amplitude oscillations.
Summary.
- Method of resonance characteristics calculation for probe-sample system is proposed. Using this technique frequency and phase shift at given oscillation amplitude can be found. It is more convenient than to solve the implicit system (1, 2).
- Using equation system (4, 5) approach-retraction curves is deduced.
- It is shown that in case of small oscillation amplitude
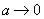 , perturbation theory coincides with theory of cantilever small oscillations.
, perturbation theory coincides with theory of cantilever small oscillations.






