1.2.2 John G. Simmons Formula in a Case of Small, Intermediate and High Voltage (Field Emission Mode).
+1-480-493-0093

1.2.2 John G. Simmons Formula in a Case of Small, Intermediate and High Voltage (Field Emission Mode).

According chapter 1.2.1, the approximate expression for the tunneling current in the MIM system can be written as [1]:

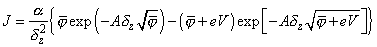
(1)

where 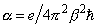, , 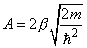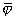– average barrier height, 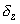– barrier width, 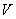– voltage between electrodes.

Small voltage.

At low voltages 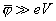, expression (1) can be simplified [1]

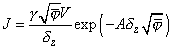
(2)

where 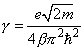. Since 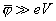, we can consider that 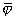doesn't depend on 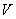. Thus, in the case of small applied voltage, the tunneling current proportionate to 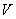. Energy diagram of the MIM system then is shown on Fig. 1.

Fig. 1. Potential barrier in the MIM system then 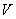~ 0.
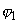and 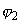– work function of the left and right metals, respectively.

Intermediate voltage.

If 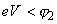, then 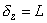and 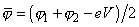(Fig. 2).

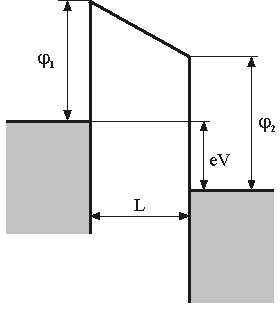
Fig. 2. Potential barrier in the MIM system then .
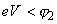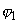and 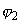– work function of the left and right metals, respectively.

In [2] it is shown, that for this case the tunneling current-voltage relation is given by

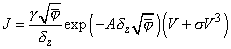
(3)

where .

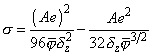High voltage – Field emission mode.

The case when 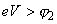corresponds to energy diagram shown in Fig. 3 and to the following , .

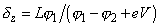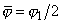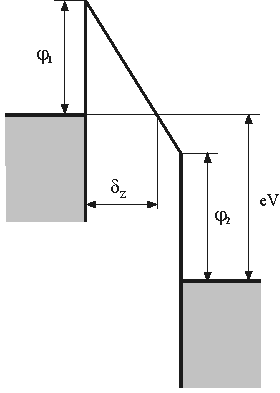
Fig. 3. Potential barrier in the MIM system then .
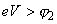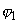and 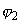– work function of the left and right metals, respectively.

Substituting 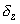and 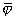into equation (1), we obtain

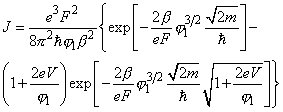
(4)

where 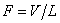– electric field strength.

At high applied voltage ( 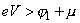) the Fermi level of electrode 2 is lower than the conduction band bottom of electrode 1. Under such conditions, electrons can not tunnel from electrode 2 into electrode 1 because of lack of empty states. An inverse situation is for electrons tunneling from electrode 1 into empty states of electrode 2. This process is similar to autoelectronic emission from a metal into vacuum. Thus, since 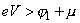, the second summand in (4) can be neglected and for the current we get

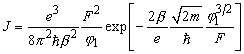
(5)

where coefficient b = 23/24. This result agrees qualitatively with an analytical expression for the field emission current density [3].

Thus, using formulas (2)–(5), we can compute the tunnel current at given system parameters and plot current-voltage characteristics. Fig. 4 shows theoretical tunneling current-applied voltage plot in case of carbon electrode 1 (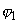 = 4,7 эВ) and platinum electrode 2 (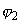 = 5,3 эВ) at 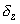= 5 Å and contact area S = 10-17 m2.

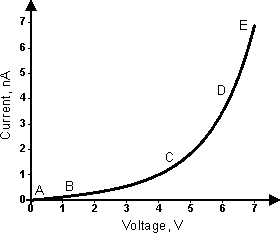
Fig. 4. Current-voltage characteristic for carbon electrode 1 and platinum electrode 2 at 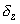= 5 Å and contact area 10-17 m2. Parts of J(V) curve correspond to the following expressions: AB – (22), BC – (23), CD – (24), DE – (25).

Summary.

  • Depend upon magnitude of applied voltage, formula (1) can be simplified (2)–(5).
  • It is possible to describe the experimental tunneling current dependences by approximated expressions (2)–(5) in accordance with magnitude of applied voltage.

References.

  1. John G. Simmons. J. Appl. Phys. - 1963. - V. 34 1793.
  2. John G. Simmons. J. Appl. Phys. - 1963. - V. 34 238.
  3. Dobretzov L.N., Gomounova M.V. Emission electronics. Nauka, 1966 (in Russian)