2.7.7 Interaction between paramagnetic probe and magnet sample
If magnetic field
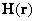 produced by a sample is known, then force
produced by a sample is known, then force
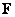 on a magnetic cantilever and its derivative
on a magnetic cantilever and its derivative
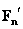 in direction
in direction
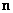 can be calculated integrating the force acting on the elementary volume
can be calculated integrating the force acting on the elementary volume
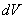 over the whole ferromagnetic film volume
over the whole ferromagnetic film volume
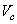 [1]:
[1]:
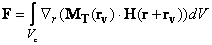
(1)
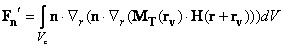
(2)
where
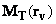 – magnetic moment of the unit volume of the cantilever magnetic coating,
– magnetic moment of the unit volume of the cantilever magnetic coating,
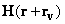 – magnetic field from the sample,
– magnetic field from the sample,
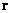 – vector corresponding to the probe's tip position,
– vector corresponding to the probe's tip position,
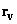 – vector corresponding to the elementary magnetic moment position relative to
– vector corresponding to the elementary magnetic moment position relative to
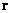 ,
,
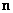 – normal vector to the probe surface collinear with its principal axis of symmetry (Fig. 1).
– normal vector to the probe surface collinear with its principal axis of symmetry (Fig. 1).
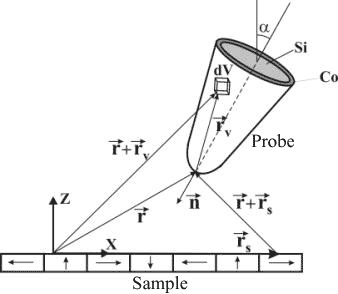
Fig. 1. The model geometry used to calculate the force and its derivative acting on a tip.
If vector
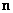 is directed along the Z-axis, then force (1) and its Z-derivative (2) can be written as
is directed along the Z-axis, then force (1) and its Z-derivative (2) can be written as
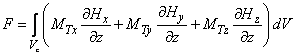
(3)
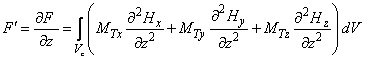
(4)
For paramagnetic materials, the magnetization vector
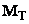 depends on external magnetic field magnitude [2]. Particularly, if external magnetic field is zero, the magnetization inside the material is zero. Otherwise, it is equal to [2]
depends on external magnetic field magnitude [2]. Particularly, if external magnetic field is zero, the magnetization inside the material is zero. Otherwise, it is equal to [2]
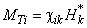
(5)
where
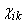 – tensor of material magnetizability,
– tensor of material magnetizability,
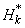 – magnetic field inside the material induced by external field
– magnetic field inside the material induced by external field
 . The relation between vectors
. The relation between vectors
 and
and
 can be obtained from boundary conditions for normal (denoted as n) and tangential (denoted as t) components of vectors
can be obtained from boundary conditions for normal (denoted as n) and tangential (denoted as t) components of vectors
 ,
,
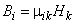 at two media interface [2]
at two media interface [2]
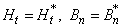
(6)
where
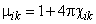 – tensor of the medium magnetic permeability. Thus, the magnetization vector of the paramagnetic probe
– tensor of the medium magnetic permeability. Thus, the magnetization vector of the paramagnetic probe
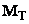 depends on external magnetic field spatial distribution in accordance with formulas (5,6).
depends on external magnetic field spatial distribution in accordance with formulas (5,6).
As an MFM tip, a carbon nanotube deposited onto the standard cantilever tip, can be used [3,4]. Carbon is a paramagnetic material, therefore, the tip magnetization is a function of external magnetic field in accordance with (5). Let us determine the magnetization of the nanotube placed in a uniform magnetic field.
The carbon nanotube is cylindrically shaped and its length is normally much more than the radius. In this case, its geometry can be approximated by an ellipsoid of revolution. The relationship between magnetic field
 inside the ellipsoid and uniform external magnetic field
inside the ellipsoid and uniform external magnetic field
 is given by [5]
is given by [5]
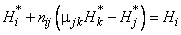
(7)
where
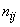 – tensor of demagnetizing factors. Then, determining
– tensor of demagnetizing factors. Then, determining
 from (7) and substituting it into (5), we can obtain the magnetization of the nanotube in the uniform magnetic field.
from (7) and substituting it into (5), we can obtain the magnetization of the nanotube in the uniform magnetic field.
Summary.
- Described is a model which allows to determine in a general case the force and its derivative acting on a paramagnetic tip with known magnetic characteristics.
- The magnetization vector of paramagnetic tip depends on spatial distribution of external magnetic field in accordance with formulas (5,6).
- Magnetization of a nanotube in a uniform magnetic field is considered.
References.
- P. Grutter, H.J. Mamin, D. Rugar, in Scanning Tunneling Microscopy II, edited by R. Wiesendanger and H.-J. Guntherodt (Springer, Berlin, 1992) pp. 151-207.
- Ch. Kittel. - "Introduction into the solid state physics", Moscow: "Nauka", 1978, 792 pp. (in Russian).
- Akita S., Nakayama Y., Arie T. Yoshida N.: J. Appl. Phys. 34, 43-45 (2001).
- Akita S., Nakayama Y., Arie T. Nishijima Hidehiro.: J. of Vacuum Science and Technology B 18, 1 (2000) 104-107.
- L.D. Landau, E.M. Lifshits - "Theoretical physics volume 8. Electrodynamics of continuum",Moscow: "Nauka", 1982, 620 pp. (in Russian).






