2.6.1 The nature of frictional forces
Lateral forces (besides normal to the surface forces) arise from the tip-surface interaction. AFM allows to measure these forces thereby expanding surface analysis ability for various samples. This technique is called the Lateral Force Microscopy (LFM).
What is the nature of lateral forces and what additional information about a surface they can reveal? There are two forces having horizontal component – frictional force
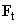 and normal load
and normal load
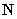 which deviates from vertical due to the surface asperities (Fig. 1).
which deviates from vertical due to the surface asperities (Fig. 1).
The latter force is entirely determined by the surface relief. Thus, lateral forces give information about the surface topography; however, existence of other developed imaging techniques lowers the experimental value of lateral forces imaging.
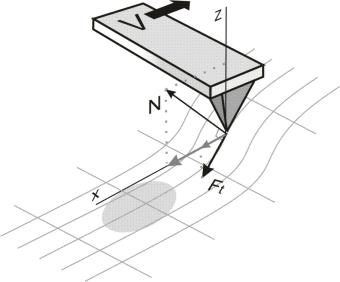
Fig. 1. The nature of lateral forces.
On the other hand, friction force study can result in obtaining new data about surface properties. This made the AFM an important tool for the tribology – the physical science studying the nature of friction.
Depending on the scale of the friction study, the modern tribology is divided into three fields:
- macrotribology (or just tribology)
- microtribology
- nanotribology
Since their emergence, the scanning microscopes offer an ability to study micro/nanotribology. Below we present some essential principles of tribology and discuss the technique of lateral forces investigation.
The frictional force is an aggregate effect arising from various physical phenomena: elasticity, adhesion, viscosity, capillary forces, surface chemistry, phononic and electrostatic interaction, etc. Any of them can dominate depending on conditions.
Each tribology field investigates friction at its own scale. Macrotribology deals with large objects and do not take into consideration a matter structure. On the contrary, nanotribology explains friction on the level of individual atoms interaction. Microtribology is an intermediate field.
The macrotribology basic law is the Amontons-Coulomb law stating that the friction force is proportional to the loading (normal) force:
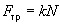 ,
,
(1)
where k – dimensionless coefficient of friction containing all the tribology information. It depends on many factors, such as temperature, humidity, sliding velocity, etc.
In macrotribology, it is considered that geometrical contact area of two bodies is equal to (or slightly differs from) the real contact area on the atomic scale. This is certainly an approximation because in fact even very flat surfaces seem rough at lower scale, so the true contact area is much less – only asperities are in perfect contact. At the macroscale, the contact is a great number of microcontacts (Fig.2). In this case, the macroscopic frictional force is an averaged microscopic frictional force of individual microcontacts that can vary greatly.
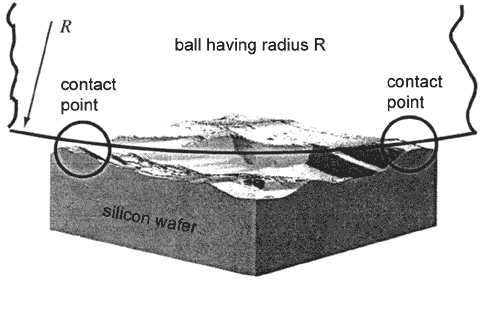
Fig. 2. Ball-silicon wafer contact on the macroscopic scale [1].
Microtribology studies such individual contacts. As a rule, it is implied that a small single asperity interacts with a surface. Namely this model made the AFM an attractive experimental tool for microtribological studies.
As it is well known, friction is the dissipative force. When the two surfaces in contact slide against each other, mechanical energy dissipation occurs. For example, to maintain constant sliding velocity, an internal force must produce work, therefore, every factor giving rise to friction has a mechanism of the energy dissipation. Considering microtribology, let us list some of them.
Friction can be either dry or wet. It is considered to be wet even when an extremely thin (few atomic layers) film of liquid occurs on the surface. Due to the adsorption this is always the case except for the following:
- hydrophobic surfaces of tip and sample;
- friction in vacuum;
- large normal load resulting in squeezing out of the liquid from the interface, true contact of surfaces establishing and actual realization of the dry friction mechanismа.
It is considered that in case of dry friction surface asperities hit against each other. While overcoming obstacles, atomic-lattice vibrations are generated and dissipated as phonons which carry away the energy. Moreover, when adhesion links between hills of surfaces in contact are broken, electron-hole pairs are created in metallic samples and this process also requires energy (this effect is much weaker than phononic dissipation). In case of soft samples, microasperities can be destroyed (the so called "plowing") and mechanical energy is spent on atomic links break.
Wet friction depends much on liquid layer thickness. If a film is monomolecular, friction is dry-like. If a film is two-three monolayers thick, the energy dissipation in a phonon channel is blocked and liquid layer viscosity is of major importance. For more thick films capillary effects predominate which results in contacting surfaces asperities attraction upon shear.
What is the relation between frictional force and loading force in microtribology? The Amontons-Coulomb low analogue here is the Bowden-Tabor relation (model) written as:
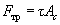
(2)
where
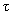 – shear stress,
– shear stress,
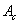 – true area of elementary contact (in contrast to geometrical contact area in macrotribology). This area depends on degree of both contacting surface hills mutual indenting. As it is known, the area of such contact is given by the Hertz theory:
– true area of elementary contact (in contrast to geometrical contact area in macrotribology). This area depends on degree of both contacting surface hills mutual indenting. As it is known, the area of such contact is given by the Hertz theory:
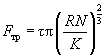
(3)
where R – tip radius of curvature, N – normal loading force, K – reduced Young's modulus, given by
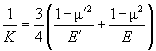
(4)
with E, E' – Young's moduli and m, m' – Poisson's ratios of tip and sample, respectively. For the silicon probe and sample
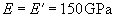 ,
,
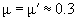 ,
,
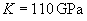 .
.
As it can be seen, dependence of the frictional force on normal load N is nonlinear. If a film of liquid exists, it is necessary to add to N an adhesion term arising from the capillary force. Using the DMT model, it can be written as:
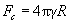
(5)
where
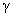 – surface tension coefficient. This is the additional attractive force between the contacting surfaces.
– surface tension coefficient. This is the additional attractive force between the contacting surfaces.
The Bowden-Tabor model is verified well in experiments. In Fig. 3 are shown experimental data [1] acquired in vacuum (lack of liquid film and capillary effect) and in air; theoretical curve (3) is presented for comparison.

Fig. 3. Experimental frictional force as a function of normal load in air and in vacuum. Thick line shows theoretical Bowden-Tabor relation [1].
In microtribology, the phenomenon such as "stick-slip" motion is frequently observed. The frictional force between the two sliding surfaces is irregular and is of saw-tooth character (Fig. 4). If a hill of one surface is stuck to a "site" of the other surface via adhesion and capillary forces, it will hardly be unstuck without predominant force. Once it is separated, it jumps (slips) into another "site" where sticks for a while and so on.
The stick-slip behaviour depends much on scan speed (Fig. 5). To investigate the dependence between frictional force and slip speed, the experiment was carried out [1]. In this experiment the frictional force was measured between silicon ball having radius 0.5 mm and flat silicon surface. Both bodies were hydrophilic. The roughness was 0.2 nm and 0.17 nm for the ball and surface respectively. At low speed the stick-slip phenomenon is pronounced, the jumps frequency is small and amplitude is large. Increasing the speed results in rising the frequency and lowering the amplitude. At some maximum critical sliding velocity the effect vanishes and frictional force becomes regular. In experiment the critical speed 0.4 mm/s was reached at normal load equal 70 mN.
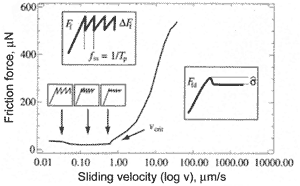
Fig. 4. Frictional force vs. sliding velocity [1]. Frictional force behavior at sliding velocities above and under critical is shown in boxes.
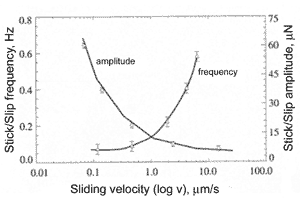
Fig. 5. Frictional force amplitude and frequency at stick-slip motion as a function of scan speed [1].
On the same samples the dependence between frictional force and temperature/humidity was studied[1]. From the beginning both solids were hydrophilic. Then, in order to remove the oxide film and make them hydrophobic, they were etched in hydrofluoric acid for two minutes.
Thus, the frictional force was measured versus relative humidity (RH) at various temperatures for hydrophilic and hydrophobic samples. The measuring system was placed into a camera with adjustable humidity and temperature. RH was in the range from 85% to 20%. The normal load was maintained constant and amounted N = 2000 mN. The results for high and low temperatures are shown in Fig. 6 [1].
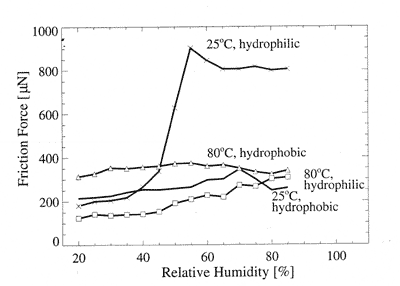
Fig. 6. Friction vs. humidity at various temperatures for hydrophilic and hydrophobic systems [1].
The hydrophilic sample can adsorb ample quantity of water. Thus, the more the environment humidity is, the more liquid can be adsorbed and the higher the frictional force is. As the temperature grows, desorption starts to prevail over adsorption and friction decreases. The more the temperature is, the more energetic water molecules are and the easier they leave the surface and return to it. That is why friction slightly depends on humidity.
Hydrophobic silicon, in contrast to the hydrophilic one, reveals weak dependence of friction on humidity at any temperature. With temperature growth, the friction slightly rises. This means that, as a result of desorption, solid surfaces are in tighter contact, Van der Waals forces start to act between them and chemical bonds arise.
Nanotribology deals with individual atoms interaction. Imagine a surface atom of one body (AFM tip) that slides in a periodic potential of surface atoms of the other body (sample) (Fig. 7) and the energy is not dissipated.
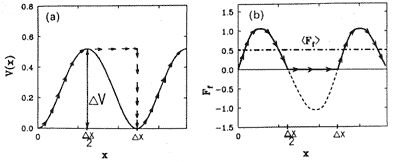
Fig. 7. Left: Potential energy and tip path.
Right: Instantaneous and average frictional force [3].
Nonconservatism is introduced as follows. Reaching the point of potential maximum, the atom, which can be modeled as a spring suspended ball, loses contact with the surface and "falls" to the point of potential minimum (or its neighborhood). The atom passes into the site with another energy, i.e. the potential becomes "nonpotential". The instantaneous frictional force in this case is
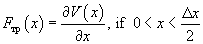
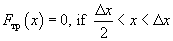
(6)
It may be thought that thanks to the spring suspension, the energy is transmitted deep into the body, i.e. from the nanoscopic point of view it is dissipated. This model leads to a nonconservative (on average) force shown in Fig. 7 which is the frictional force. This averaged nonconservative force is considered to be the frictional force in microtribology.
As an example, we present experimental data [2], [4] (Fig. 8) obtained for highly oriented pyrolytic graphite (HOPG).
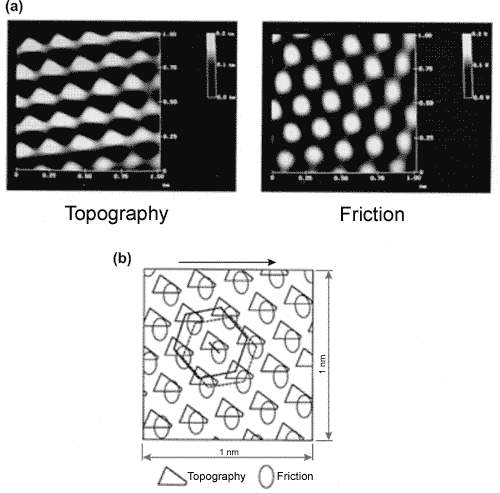
Fig. 8. (a) Topography and frictional force images for the HOPG sample sized 1 nm x 1 nm. (b) Schematic overlay of the two images.
Symbols mark corresponding maximums. Spatial shift between images is clearly seen [2], [4].
It is seen that the surface topography and frictional force image are of the same periodicity and shifted relative each other in accordance with the above presented theory.
Notice that the HOPG surface should be dry. Water adsorption in this case is of greater significance than on the microscopic scale. Capillary forces damp stick-slip motion so the acquired image becomes fuzzy.
Summary.
- The science of friction – tribology – is subdivided into macrotribology, microtribology, and nanotribology. To describe friction at different scales, various models are used.
- The friction depends sufficiently on humidity, temperature, adsorption, etc. and can be of dry or wet type.
- The basic equation of macrotribology is the Amontons-Coulomb law. The macroscopic area of contacting bodies is considered to be multiple elementary contacts whose total area is much less than the gross contact area.
- Dry friction in the elementary contact is described by the Bowden-Tabor model. It employs the Hertzian theory on the elastic deformation in place of contact, the friction parameter being the shear stress.
- Capillary forces are of major importance in the wet friction.
- In microtribology, "stick-slip" phenomenon results in the frictional force irregularity and its saw-toothed variation.
- The nanotribology describes friction in terms of atoms interaction. Considering the motion of one body atoms in the potential of the other body atoms, it is possible to introduce the nonconservative force describing friction.
References.
- Scherge Matthias, Biological micro- and nanotribology: Nature's solutions. Springer, 2001
- N.P. D'Costa, J.H. Hoh, Rev. Sci.Instrum. 66 (1995) 5096-5097
- Wiesendanger R., Guentherodt H.-J. (eds.), Scanning tunneling microscopy. - 2d ed. 3 : Theory of STM and related scanning probe methods. 1996
- Bhushan B., Wear 225-229 (1999) 465-492.






