2.2.4.1 Intermolecular Van der Waals force

The Van der Waals force or the intermolecular attractive force has three components of slightly different physical nature but having the same potential dependence on the intermolecular distance – . This lucky circumstance allows to compare directly constants of interaction that correspond to three Van der Waals force components because proportions between them will be held constant at different magnitudes. Constants at multiplier will differ for various materials.

(1)

All three Van der Waals force components are based on dipoles interaction, therefore we should remember two basic formulas:

the energy of dipole placed in field is [1]:

(2)

and the electric field produced by the dipole is [1]:

(3)
where n – unit vector directed from the point at
which the energy is determined to the dipole.

The orientational interaction (or the Casimir force) arises between two polar molecules each of which has the electric dipole moment. In accordance with (2), (3) the interaction energy of dipoles and separated by distance

(4)

depends sufficiently upon the molecules relative position. Here is the unit vector directed along the line between molecules.

In order to reach the potential minimum, dipoles tend to align along the common axis (Fig. 1). The thermal motion, however, breaks this order. To determine the "resulting" orientation potential one should average statistically interactions over all possible orientations of molecules pair. Notice that in accordance with the Gibbs distribution , which gives the probability of the system being in the state with energy at temperature , the energetically advantageous orientations are preferable. That is why despite the isotropy of possible mutual orientations, the average result will be nonzero.

Fig. 1. The energy of dipoles interaction depends on their mutual orientation.
To find the "effective" potential it is necessary to perform the thermodynamic averaging over all directions of dipoles in space.

Averaging with the use of the Gibbs distribution is performed in accordance with the following formula:

(5)

where, for the sake of normalization, the denominator is the statistical sum and is the integration parameter providing enumeration of all the system possible states (a pair of dipoles mutual orientations).

If the exponent can be approximated by the series expansion:

(6)

so the energy of orientation interaction is approximated as:

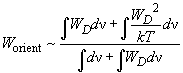
(7)

On performing integration it can be shown that , thus, 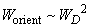. Introducing constant in accordance with (4), we finally have:

(8)

The induction interaction (or the Debye force) arises between polar and nonpolar molecules. Electric field generated by dipole polarizes the other molecule (Fig. 2). The induced moment calculated in the first order of the quantum perturbation theory is equal to 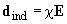where stands for the molecule polarizability.

Fig. 2. Under the polar molecule field the neighboring one acquires the induced dipole moment.

Then, the potential of induction interaction is computed as follows:

(9)

Thus, this kind of interaction also "universally" depends on though having the other reason and the other constant.

It should be noted that in liquids and solids the polarized molecule experiences the symmetric influence of many neighbor molecules, the induction interaction being strongly compensated by their action. The result is that the real induction interaction is estimated as:

(10)

The dispersion interaction (or the London force) is a prevailing one because it involves nonpolar molecules as well. This third term in (1) is always presented that is why it is the major one.

Fig. 3. Due to the quantum uncertainty, nonpolar molecules have "momentary" dipole moments, interaction
between which is of the second order of smallness of the perturbation theory.

In a system of nonpolar molecules the electrons wave function is such that average values of dipole moments in any state are equal to zero: . However, nondiagonal matrix elements are nonzero. Moreover, the second quantum mechanical correction to the interaction energy calculated as is known [2] according to the formula below, is nonzero too:

(11)

where perturbation is given by (4), , 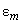– energies of the system of two molecules in arbitrary states and .

In a certain sense, "momentary" magnitudes of dipole moments (at zero average value) are nonzero and they interact (Fig. 3). In the second order of smallness the averaged magnitude of such "momentary" potential is not already vanished and namely this is the potential of dispersion interaction.

Correction (11) as is seen, is proportional to the square of perturbation . From this it is clear that

(12)

Constant is called the Hamaker constant (here , – ionization potentials, , – molecules polarizability).

The classical interpretation of this interaction is as follows. The dipole moment of one molecule arisen from fluctuations, generates field which, in turn, polarizes the second molecule. The already nonzero field of the second molecule polarizes the first one. The potential of this peculiar system with a "positive feedback" is calculated similarly to the induction interaction.

Relative values of Van der Waals force components are presented in Table 1 [3].

Substance
	0.667	0	13.6	0	0	6.3
	1.57	0	13.6	0	0	41.3
	1.74	0	15.8	0	0	59.3
	1.6	0	15.8	0	0	48
	0.2	0	24.7	0	0	1.2
	1.99	0.12	14.3	0.0034	0.057	67.5
	2.63	1.03	13.7	18.6	5.4	105
	1.48	1.84	18.0	197	10	48.8
	2.24	1.5	11.7	87	10	72.6

Table 1. Magnitudes of polarizability, dipole moment, ionization potential and energies of different weak interactions between various atoms and molecules.

Obviously, the force is determined by

(13)

Estimations of the Van der Waals attraction for AFM studies in the contact mode give: .

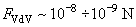Summary.

The Van der Waals force which arises from the electrostatic interaction of molecular shells has three components: orientation, induction and dispersion interactions.
Despite the different nature of the Van der Waals force components, their dependence on distance is of the same character – .

References.

Sivukhin D.V. General physics course: Electricity – Moscow. Nauka Publ., 1983. – 687 pp (in Russian)
Landau L.D. Quantum mechanics: Nonrelativistic theory. – Moscow.: Nauka Publ., 1989. – 767 pp (in Russian)
Rubin A.B. Biophysics: Theoretical biophysics. – Moscow.: Knizny dom Universitet, 1999. – 448 pp (in Russian)