2.2.3.2 Capillary force acting on the probe
Let us examine the effect of the surface tension on AFM measurements. [1]At the moment of a cantilever contact with a liquid film on a flat surface, the film surface reshapes producing the "neck". The water wets the cantilever surface (Fig. 1) because the water-cantilever contact (if it is hydrophilic) is energetically advantageous as compared to the water-air contact. Notice that in such cases the contact angle is always less than
.
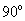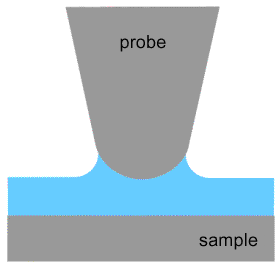
Fig. 1. "Neck" formation.
It is intuitively clear that the neck curved surface will tend to flatten that is available only at the expense of the cantilever pulling down. This means that the cantilever attracts to the sample.
Calculation of this attraction force is a simple task. Let the tip curvature radius be much larger than other characteristic dimensions of the case. In Fig. 2 the following designations are introduced:
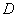– tip-sample separation,
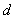– "immersion depth",
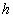– film thickness,
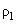– lesser curvature radius of the liquid surface,
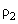– tip-liquid contact area radius.
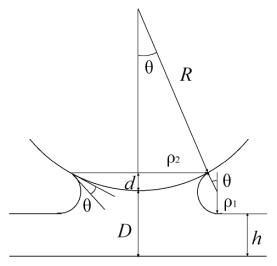
Fig. 2. On the calculation of the capillary force.
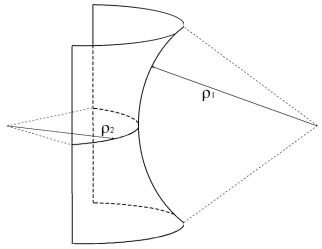
Fig. 3. Explanation of the Laplace formula.
According to the Laplace formula the pressure in liquid will be less than the atmospheric pressure by the following value:
,
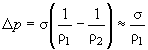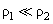
(1)
This pressure is applied to the tip-liquid interface having square
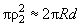. The force of the cantilever attraction to the sample due to the capillary effect is equal to:
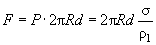
(2)
It is easy to find that
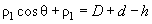(for the sake of simplicity we assume contact angles
for the tip and the sample to be equal). Then we get:
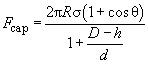
(3)
If we neglect the liquid film thickness (
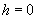), then the equation
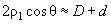is valid and formula (6) is simplified to [1]:
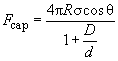
(4)
We will not concentrate attention on
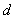value determination. For the estimation purpose we will use the maximum value of the capillary attraction force that takes place at
. In this case the unknown parameter
vanishes:
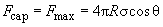
(5)
Taking into account that cantilever radius
is
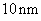, water surface tension at
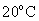is equal to
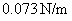and the contact angle is small i.e.
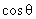is close to 1, we get the following estimation:
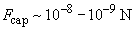. Thus, the capillary force by the order of magnitude is the same as the Van der Waals interaction and the electrostatic force.
During the cantilever approach-retraction cycle, the hysteresis arises. At the upward move the neck stays longer because the cantilever surface is already wetted and the liquid neck goes with the tip. As bonds break, the capillary force stops to act and the cantilever suddenly returns into its undeflected state.
Fig. 4. Plot of the cantilever deformation as a function of the tip-sample separation.
The hysteresis is shown which arises during the cantilever approach-retraction cycle.
The cantilever deflection
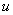vs. the distance to the sample
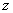is shown in Fig. 4. At large distances there is no deflection and the plot is horizontal. The left portion of the plot is linear with a slope of
. This corresponds to the contact with the surface i.e. the tip is pressed into the sample and the cantilever deflects towards the surface linearly.
As the cantilever is retracted away from the surface, the tip remains stuck to the sample: the capillary force holds it and the linear deflection-distance dependence extends below the horizontal axis until the neck disappears. After that the cantilever sharply flips off and becomes undeflected.
Summary.
- Due to the film of liquid frequently presented on the sample surface, the capillary force arises which attracts the probe to the surface.
- To quantify the capillary force it is enough to know the tip geometry and the surface tension coefficient of the liquid.
- When the cantilever is retracted from the surface the hysteresis is observed due to the liquid necking.
References.
- Israelachvili J.N. Intermolecular and Surface Forces. – Academic Press, 1998. – 450 p.