2.2.3.1 Basic principles of the surface tension theory
+1-480-493-0093

2.2.3.1 Basic principles of the surface tension theory

In most cases, the sample under investigation contains on its surface a microscopic liquid film which affects much the cantilever interaction with the surface because the surface tension force is of great importance on a microscale.

It is generally known that any interface is characterized by the free energy which is proportional to its surface :

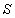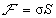
(1)

where 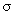– coefficient of surface tension (dyne/cm). It is clear that expressions like (1) should be written for all surfaces of the system. At equilibrium, the free energy is minimal so interfaces reshape in order to minimize the total 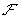value.

Consider two consequences of this principle which will give us not only the intuitive understanding of phenomena but provide with necessary formulas.

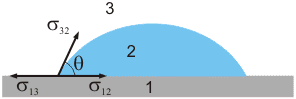
Fig. 1. Contact angle in case when one of surfaces is solid.

The boundary line of three media is characterized by the so called contact angle 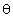(Fig. 1). If one of the surfaces is solid, the Neumann relation [1] is applied:

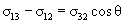
(2)

Subscripts denote the media separated by the surface with a given coefficient of surface tension (CST). Actually, formula (2) arises from the demand of the free energy minimum. One can verify that any deviation of 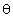in relation (2) will result in such an interface area change that 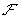will increase.

The second consequence is the curved surface pressure appearance. Consider a local flat surface area. It is clear that any deformation gives rise to its square and, hence, 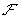increase. In order to minimize the free energy the curvature will tend to decrease which is the evidence of the curved surface pressure appearance. The corresponding Laplace formula for the difference between inside and outside pressure of a liquid is rather simple [1]:

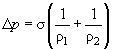
(3)

where 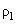and 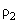– surface curvature radii in orthogonal planes (Fig. 2). If center of the curvature is positioned outside liquid, 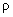is taken negative.

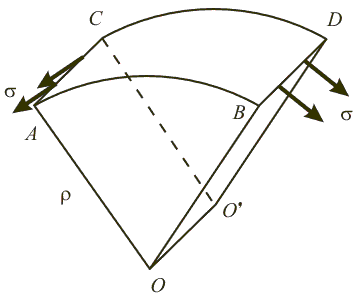
Fig. 2. Liquid surface element.

Summary.

  • At the interface between three media the contact angle arises which is determined by coefficients of surface tension and is calculated according to the Neumann formula (2).
  • The curved liquid surface produces additional pressure calculated according to the Laplace formula (3).

References.

  1. Sivukhin D.V. General physics course: thermodynamics and molecular physics. – Moscow. Nauka Publ., 1983 – 551 pp.