2.2.2.1 The Hertz problem definition
+1-480-493-0093

2.2.2.1 The Hertz problem definition

When the cantilever and the sample are in contact, elastic forces start to act giving rise to both the sample and tip deformations which can affect the acquired image. To properly interpret the results and choose the measuring mode one should have a clear idea of elastic interactions in contact and "semicontact" modes.

Such consideration is necessary in order to:

  • avoid tip or sample damage during scanning - even at low loading force the pressure in a contact zone can exceed the strength limit because contact area is very small.
  • reconstruct properly the sample surface topography basing on the acquired image profile in case when surface features are of the same size as the tip curvature radius.
  • analyze forces in the "semicontact" mode at a moment of the tip contact with the surface which directly affect the cantilever oscillation and are one of the damping reasons.

Elastic deformations in the contact zone (the Hertz problem).

Let us consider first only the elastic force. The Hertz problem is deformations determination at local contact of bodies under load 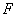action.

We have to adopt some simplifying assumptions [1].

  1. Suppose that both the cantilever and sample materials are isotropic, i.e. their elastic properties are described only by two pairs of parameters – Young's moduli 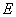, 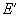and Poisson ratios 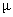, 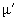. (For the anisotropic materials the number of such independent elastic characteristics can reach 21).
  2. Assume that in the vicinity of the contact point the undeformed parts of bodies surface in perpendicular planes orthogonal to the plane in the given point (Fig. 1) are described by two curvature radii 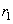, 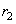(for the tip) and 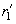, 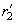(for the studied sample area).
  3. Deformations are small compared to surfaces curvature radii.

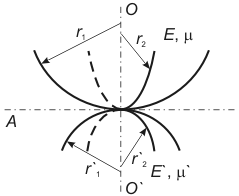
Fig. 1. Hertz problem definition.

Summary.

  • The Hertz problem solution allows to determine deformation parameters at a "point" of two bodies contact.
  • The definition of the Hertz problem stipulates that the model of isotropic elastic media is used and deformations are small.

References.

  1. Landau L.D., Livshits E.M. Theory of elasticity. – Nauka, 1987. – 246 p. (in Russian)